اتحاد مربع دوجمله ای

  در ادامه مباحث مربوط به ویدئوهای آموزش ریاضی نهم که قسمتی از آموزش ریاضی نهم نیز می باشند به آموزش درس اول فصل پنجم ریاضی نهم یعنی مبحث اتحاد و فاکتور گیری می رسیم. در فصل پنجم ریاضی نهم، با مفهوم اتحادها آشنا می شویم و روش ساده کردن و تبدیل عبارت های جبری به اتحادها را یاد میگیریم. اتحاد مربع دوجمله ای، اتحاد مزدوج از جمله آموزش های این فصل می باشد.

اتحاد جبری چیست ؟

اگر به دو عبارت جبری به ازای هر یک از متغیرهایشان، هر مقداری داده شود، آن دو عبارت جبری با هم برابر باشند، به این تساوی اتحاد جبری گفته می شود. به عبارت ساده تر اگر دو عبارت جبری داشته باشیم به گونه ای که مقدار هر دو عبارت جبری با دادن هر عدد یکسان  به متغیرهای آن عبارت های جبری، با هم برابر شوند، می توان گفت که دو عبارت جبری با یکدیگر متحد هستند. اتحاد جبری نیز به برابری آن دو عبارت جبری گفته می شود. برای اینکه مفهوم اتحاد جبری برایتان کاملاً روشن شود، به این جدول و مثال های آن دقت کنید. به ازای متغیر داخل عبارت های جبری مقدار یکسانی می دهیم و جواب هایی که با هم برابر هستند، یعنی آن دو عبارت جبری، اتحاد جبری هستند. نکته خیلی مهم:

تفاوت اتحاد جبری با معادله

اتحاد جبری به ازای تمامی مقادیر می تواند برقرار باشد ولی در معادله فقط تعداد محدودی از مقادیر وجود دارد که به ازای آنها، آن معادله با معنی و دارای جواب خواهد بود. یکی از آموزش هایی که پیشنهاد می کنیم ببینید، جمع و تفریق رادیکال ها است. آن را از دست ندهید.

اتحاد مربع دو جمله ای

مفهوم اتحاد مربع دوجمله ای به این معنا است که مربع ( توان 2 ) مجموع یا تفاضل دو جمله برابر است با: جمله اول به توان 2 به علاوه یا منهای 2برابر جمله اول در جمله دوم به علاوه مربع ( توان 2 ) جمله دوم. اگر بخواهیم اتحاد دوجمله ای را به زبان ریاضی نشان دهیم به این صورت خواهد بود.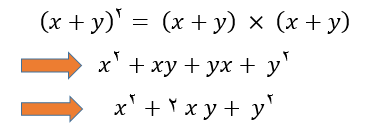 مطمئن هستم که خودتان هم می توانید تساوی این رابطه را ثابت کنید. حالا یکبار باهم مرور می کنیم.

نکات مهم و امتحانی اتحاد دو جمله ای

طراحان سوال در خصوص درس اول فصل پنجم ریاضی نهم یعنی اتحاد مربع دوجمله ای یا همان اتحاد دوجمله ای به موارد زیر، دقت و نگاه ویژه ای دارند. شما همیشه این نکات متحانی در مورد اتحاد دوجمله ای را در نظر داشته باشید. برای دانلود نمونه سوال فصل پنجم ریاضی نهم هم می توانید به صفحه مربوطه رجوع کنید. نکته 1: اگر با یک عبارت سه جمله ای مواجه شدید که ضریب یکی از جملات آن زوج بود، حتماً برای تجزیه آن عبارت، قبل از بقیه روشها، اتحاد دو جمله ای را امتحان کنید. نکته 2: اگر در یک عبارت سه جمله ای، دو جمله آن دارای دو توان زوج بودند، بهترین گزینه برای تجزیه آن عبارت، استفاده از اتحاد دوجمله ای است. نکته 3: در عبارت های دوجمله ای که یکی از جمملات رادیکالی و دیگری غیر رادیکالی باشد، معمولاً این عبارات تجزیه شده یک اتحاد مربع دو جمله ای هستند. این دو جمله از مجموع سه جمله به دست آمده است که دو تای آنها عدد گویا و دیگری گنگ بوده است. در نتیجه به جای سه جمله تنها دو جمله را می بینید. برای گویا بودن نکته سوم به مثال زیر توجه کنید. 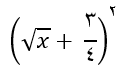مثال1: حاصل عبارت را با استفاده از اتحاد مربع دوجمله ای به دست آورید. حل: برای حل این عبارت، ابتدا فرمول اتحاد دوجمله ای را پیاده کنید و مرحله به مرحله ساده کنید. 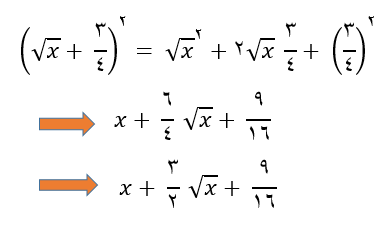مثال2: حاصل عبارت 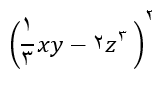را با استفاده از اتحاد مربع دوجمله ای به دست آورید. 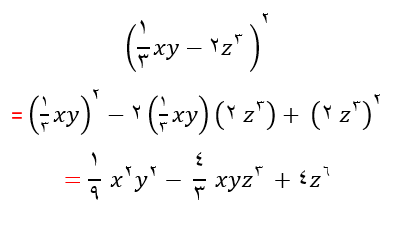برای یادگیری بهتر این مبحث مثال های بیشتری را حل کنید تا به صورت کامل به این درس تسلط پیدا کنید. می توانید از بهترین کتاب کار ریاضی نهم کمک بگیرید و اگر سوالی داشتید، کامنت کنید.