مجموعه های برابر و نمایش مجموعه ها ( برابری مجموعه ها )

مجموعه‌های برابر ریاضی نهم

پس از اینکه معرفی مجموعه ها ریاضی نهم را یاد گرفتیم به مبحث برابری مجموعه ها می رسیم.

به همراه 3 ویدئوی رایگان از سری ویدئوهای پکیج آموزش ریاضی نهم این درس را با هم پیش خواهیم برد. اگر سوالی برایتان پیش آمد حتما در ادامه برایمان کامنت بگذارید.

دو مجموعه برابر ریاضی نهم

دو مجموعه A و B با هم برابر و  یکسان هستند اگر، هر عضو مجموعه A در مجموعه B و هر عضو مجموعه B در مجموعه A باشد. به عبارت دیگر A=B باشد.

اگر عضوی در مجموعه A باشد که در مجموعه B نیست یا بالعکس، آنگاه دو مجموعه نابرابر هستند. به عبارتی همه اعضای مجموعه A باید با اعضای مجموعه B برابر باشند.

تعریف مجموعه نابرابر: هنگامی دو مجموعه A و B نا مساوی‌اند که، حداقل یک عضو در مجموعه A باشد که در B نباشد و بالعکس.

مثال 1: جا‌های خالی را طوری پر کنید که دو مجموعه روبرو برابر باشند. {…، رادیکال 16 ،5}={…، 3،4}

حل: اول نکات این مساله را با هم مشخص می کنیم. رادیکال 16 = 4. به همین راحتی دو عضو برابر را توانستیم تشخیص دهیم. پس جاهای خالی را به شکل زیر پر می کنیم.

{3، رادیکال 16 ،5}= A

{5، 3،4} = B

مثال 2: برای تشخیص مجموعه های نابرابر این ویدئو را ببینید تا کاملاً با مفهوم برابری مجموعه ها و مجموعه های نابرابر آشنا شوید.

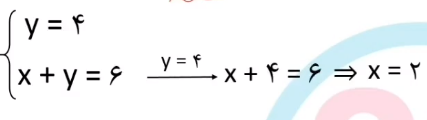
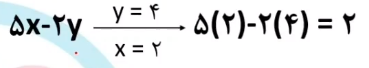
برای حل نمونه سوالات بیشتر یا نیاز به تدریس خصوص ریاضی با ما تماس بگیرید.

زیرمجموعه ریاضی نهم

یکی دیگر از مباحث مجموعه های برابر ریاضی نهم، زیرمجموعه است. یکی از مباحث شیرین که در درس دوم فصل اول ریاضی نهم تدریس می شود، مفهوم زیرمجموعه است. ابتدا این ویدئوی آموزش زیرمجموعه را ببینید.

تعریف زیرمجموعه ریاضی نهم درس دوم

8 نکته مهم در خصوص زیرمجموعه ها

اگر مجموعه A را به عنوان مجموعه مادر در نظر بگیریم، A={1،{2}،3}

1- زیرمجموعه A ، تنها اعضای موجود در مجموعه مادر را می تواند داشته باشد.

2- زیرمجموعه، هیچ عضوی بیشتر از مجموعه مادر نمی تواند داشته باشد و تعداد اعضای آن نباید بیشتر از مجموعه مادر باشد.

3- برای نوشتن زیرمجموعه، حتماً باید عضو داخل آکولاد باشد. یعنی 3 زیر مجموعه A نیست ولی {3} زیرمجموعه A است. {2} زیرمجموعه A نیست ولی {{2}} زیرمجموعه A است. به نکات انحرافی باید دقت داشته باشید.

4- برای نوشتن زیرمجموعه های یک مجموعه از کوچکترین زیرمجموعه شروع به نوشتن می کنیم که زیرمجموعه ها از قلم نیوفتند.

5- تهی زیرمجموعه هر مجموعه ای است.

6- هر مجموعه زیرمجموعه خودش است و بزرگترین زیرمجموعه هر مجموعه خودش است.

7- تعداد زیرمجموعه های یک مجموعه n عضوی از فرمول 2 به توان n به دست می آید.

8- هر دو مجموعه برابر، زیرمجموعه هم هستند. زیرا به ازای هر X∈A داریم X∈B. پس A⊆B. هر عضوی از B نیز در A هست. پس B⊆A.

زیرمجموعه تهی

در نکته 5 هم گفته شد که تهی زیرمجموعه هر مجموعه ای است.

نمایش مجموعه با نماد ریاضی درس دوم ریاضی نهم

برای نمایش مجموعه ها می توانیم از نمادهای ریاضی و زبان ریاضی استفاده کنیم. به مثال زیر توجه کنید.

مجموعه D={3,4,5,6} را در نظر بگیرید که اعضا آن اعداد طبیعی هستند. آن را به زبان ریاضی بنویسید. 

چون در صورت سوال گفته شده است که اعضای مجموعه از اعداد طبیعی هستند پس شرط اول در نوشتن مجموعه به زبان ریاضی، این است که اعضا عضو مجموعه اعداد طبیعی Nباشند. شرط دوم این است که اعضا بین 2 و 7 باشند.

D={x∈N|2<x<7}