0
از 0 رأی
رایگان!
این دوره ضبط شده توسط استدیو 20شو می باشد و حق کپی رایت آن محفوظ است
درصد پیشرفت دوره

مهسا زنده دل
درباره مدرس دارای مدرک کارشناسی ارشد هوش مصنوعی و ۸ سال سابقه تدریس ریاضی و تیزهوشان از مقطع ششم تا نهم به صورت حضوری و آنلاین. مبتکر آموزش به شیوه خلاقانه با...
مشاهده بیشترمعادله خط شیب و عرض از مبدا آموزش ریاضی نهم
منتشر شده در 1400/05/10 0 نظر
به روز شده در 1402/02/07
در فصل ششم ریاضی نهم مربوط به معادله خط ( شیب و عرض از مبدا ) ابتدا یاد می گیریم که فرمول خط استاندارد به چه صورت است. سپس روش های حل مسائل مربوط به معادله خط را با هم مرور می کنیم. برای تهیه پکیج آموزش ریاضی نهم با تدریس مهسا زنده دل کلیک کنید.
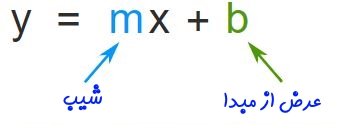 b همان عرض از مبدا و a شیب خط می باشد. دقت داشته باشید که در معادله خط به صورت استاندارد ضریب y حتماً باید یک ( 1 ) باشد.
b همان عرض از مبدا و a شیب خط می باشد. دقت داشته باشید که در معادله خط به صورت استاندارد ضریب y حتماً باید یک ( 1 ) باشد.
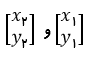 باید از این فرمول استفاده کنید.
باید از این فرمول استفاده کنید.
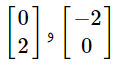 بر روی خط b و دو نقطه
بر روی خط b و دو نقطه 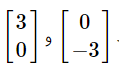 بر روی خط r قرار دارند. با فرض اینکه دو خط r و b با هم موازی هستند، شیب خطوط را به دست آورید.
حل: برای به دست آورن شیب خط کافی است که مختصات دو نقطه از آن را داشته باشیم. بنابراین با استفاده از فرمول شیب خط که در ابتدا توضیح دادیم، به راحتی می توانید این سوال را حل کنید.
بر روی خط r قرار دارند. با فرض اینکه دو خط r و b با هم موازی هستند، شیب خطوط را به دست آورید.
حل: برای به دست آورن شیب خط کافی است که مختصات دو نقطه از آن را داشته باشیم. بنابراین با استفاده از فرمول شیب خط که در ابتدا توضیح دادیم، به راحتی می توانید این سوال را حل کنید.
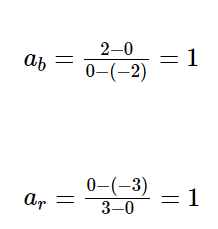 اگر بر روی نمودار دو خط را با مختصات داده شده رسم کنید، می بینید که دو خط موازی بوده و شیب های برابر دارند.
اگر بر روی نمودار دو خط را با مختصات داده شده رسم کنید، می بینید که دو خط موازی بوده و شیب های برابر دارند.
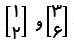 می گذرد ، را بنویسید.
برای حل سوالات اینچنین، ابتدا با استفاده از فرمول شیب خط، شیب خط را پیدا می کنیم . در این مثال:
می گذرد ، را بنویسید.
برای حل سوالات اینچنین، ابتدا با استفاده از فرمول شیب خط، شیب خط را پیدا می کنیم . در این مثال:
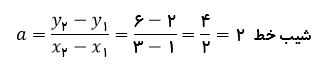 بله درسته شیب برابر است با عدد 2.
حالا برای نوشتن معادله خط به عرض از مبدا هم نیاز داریم. بیایید با استفاده از مختصات یکی از اعداد مطرح شده در سوال، معادله خط را بازنویسی کنیم و عرض از مبدا را پبدا کنیم. به طور مثال نقطه
بله درسته شیب برابر است با عدد 2.
حالا برای نوشتن معادله خط به عرض از مبدا هم نیاز داریم. بیایید با استفاده از مختصات یکی از اعداد مطرح شده در سوال، معادله خط را بازنویسی کنیم و عرض از مبدا را پبدا کنیم. به طور مثال نقطه 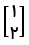 را انتخاب می کنیم. y این نقطه برابر 2 هست، شیب را هم قبلاً پیدا کردیم و برابر 2 بود. با توجه به مختصات نقطه داده شده، x برابر 1 هست. پس معادله خط به این شکل می شود
را انتخاب می کنیم. y این نقطه برابر 2 هست، شیب را هم قبلاً پیدا کردیم و برابر 2 بود. با توجه به مختصات نقطه داده شده، x برابر 1 هست. پس معادله خط به این شکل می شود
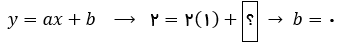 خب الان معادله ما یک مجهول دارد و جواب آن 0 ( صفر ) هست. یعنی عرض از مبدا این معادله خط برابر 0 هست.
جواب سوال معادله خط برابر است با :
خب الان معادله ما یک مجهول دارد و جواب آن 0 ( صفر ) هست. یعنی عرض از مبدا این معادله خط برابر 0 هست.
جواب سوال معادله خط برابر است با :
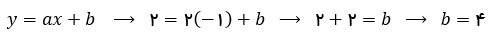 معادله خط با استفاده از اطلاعاتی که به دست آوردیم به این حالت می شود.
معادله خط با استفاده از اطلاعاتی که به دست آوردیم به این حالت می شود.
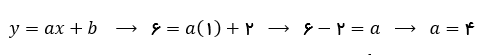 به همین راحتی شیب خط یعنی a را به دست آوردیم و می توانیم معادله خط را بنویسیم.
به همین راحتی شیب خط یعنی a را به دست آوردیم و می توانیم معادله خط را بنویسیم.
 اگر دوست داری برای امتحان ریاضی آماده شوید و همه مسائل را به خوبی حل کنید، پیشنهاد می کنم تدریس خصوصی ریاضی مدرسان 20شو را از دست ندهید.
همانطور که در ویدئوی آموزش نوشتن معادله خط با استفاده از شیب و مختصات یک نقطه توضیح داده شد، برای نوشتن معادله خط سه حالت وجود دارد یا بهتر است بگوییم که سه نوع سوال امتحانی در مورد نوشتن معادله خط وجود دارد، که ما سعی کردیم مثال های متنوعی از هر سه حالت را داشته باشیم.
مثال: در این ویدئو به شما آموزش داده می شود که چطور معادله خط را به روش هندسی و در عرض چند دقیقه بنویسید. اول باید عرض از مبدا و شیب خط را مشخص کنید.
اگر دوست داری برای امتحان ریاضی آماده شوید و همه مسائل را به خوبی حل کنید، پیشنهاد می کنم تدریس خصوصی ریاضی مدرسان 20شو را از دست ندهید.
همانطور که در ویدئوی آموزش نوشتن معادله خط با استفاده از شیب و مختصات یک نقطه توضیح داده شد، برای نوشتن معادله خط سه حالت وجود دارد یا بهتر است بگوییم که سه نوع سوال امتحانی در مورد نوشتن معادله خط وجود دارد، که ما سعی کردیم مثال های متنوعی از هر سه حالت را داشته باشیم.
مثال: در این ویدئو به شما آموزش داده می شود که چطور معادله خط را به روش هندسی و در عرض چند دقیقه بنویسید. اول باید عرض از مبدا و شیب خط را مشخص کنید.
معادله خط استاندارد چیست ؟
y = ax + b
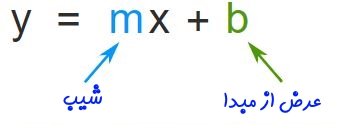 b همان عرض از مبدا و a شیب خط می باشد. دقت داشته باشید که در معادله خط به صورت استاندارد ضریب y حتماً باید یک ( 1 ) باشد.
b همان عرض از مبدا و a شیب خط می باشد. دقت داشته باشید که در معادله خط به صورت استاندارد ضریب y حتماً باید یک ( 1 ) باشد.
شیب خط چیست؟
شیب خط گذرنده بر دو نقطه برابر است با تغییرات عرضی دو نقطه، تقسیم بر تغییرات طولی همان دو نقطه. برای پیدا کردن شیب خط با استفاده از دو نقطه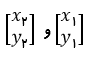 باید از این فرمول استفاده کنید.
باید از این فرمول استفاده کنید.
مثال شیب خط و عرض از مبدا ریاضی نهم
همانطور که در ویدئو هم توضیح داده می شود معمولا طراحان سوال از مبحث معادله خط به سه حالت سوال طرح می کنند.نوشتن معادله خط از طریق شیب و مختصات یک نقطه
نوشتن معادله خط با داشتن عرض از مبدا و مختصات یک نقطه
نوشتن معادله خط با داشتن مختصات دو نقطه یا یک خط
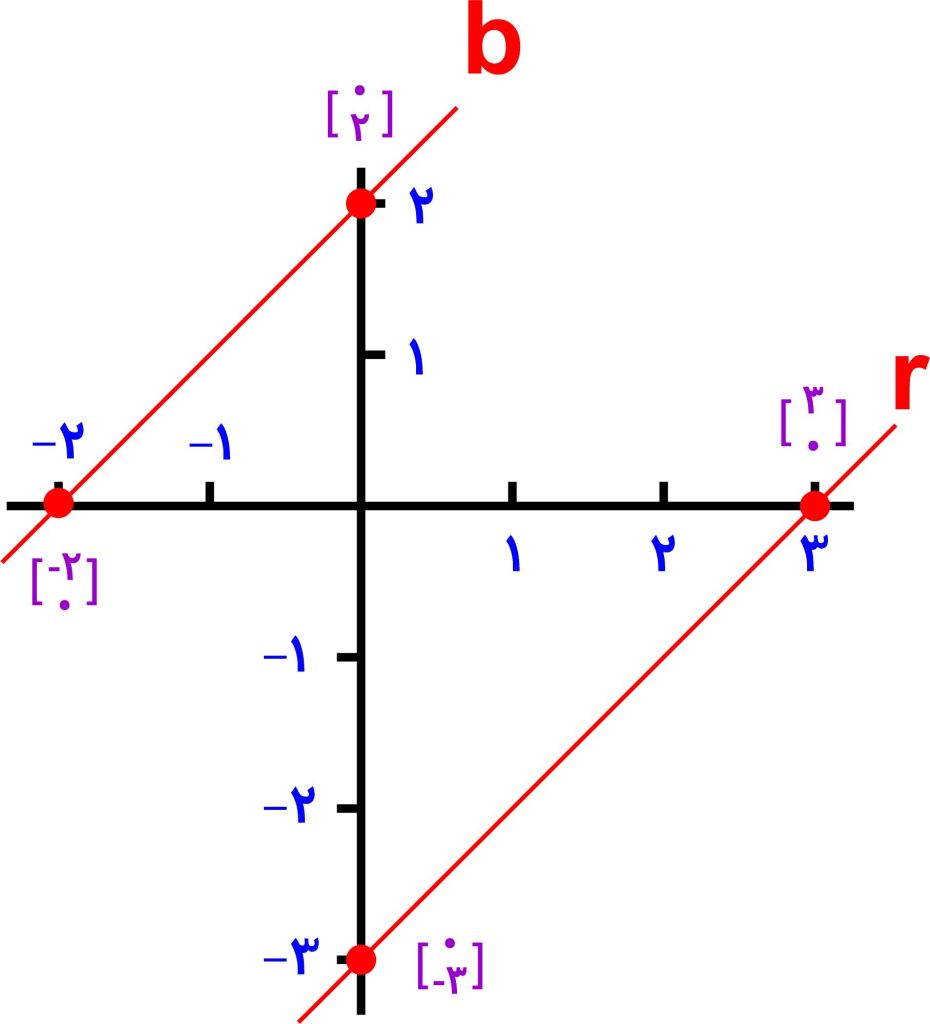
نکته 1: شیب دو خط موازی با هم برابر می باشند. از این نکته طراحان سوال استفاده کرده و ممکن است به این صورت سوالی را برای شما مطرح کنند. مثال: دو نقطه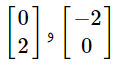 بر روی خط b و دو نقطه
بر روی خط b و دو نقطه 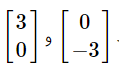 بر روی خط r قرار دارند. با فرض اینکه دو خط r و b با هم موازی هستند، شیب خطوط را به دست آورید.
حل: برای به دست آورن شیب خط کافی است که مختصات دو نقطه از آن را داشته باشیم. بنابراین با استفاده از فرمول شیب خط که در ابتدا توضیح دادیم، به راحتی می توانید این سوال را حل کنید.
بر روی خط r قرار دارند. با فرض اینکه دو خط r و b با هم موازی هستند، شیب خطوط را به دست آورید.
حل: برای به دست آورن شیب خط کافی است که مختصات دو نقطه از آن را داشته باشیم. بنابراین با استفاده از فرمول شیب خط که در ابتدا توضیح دادیم، به راحتی می توانید این سوال را حل کنید.
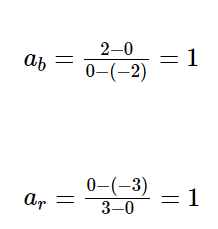 اگر بر روی نمودار دو خط را با مختصات داده شده رسم کنید، می بینید که دو خط موازی بوده و شیب های برابر دارند.
اگر بر روی نمودار دو خط را با مختصات داده شده رسم کنید، می بینید که دو خط موازی بوده و شیب های برابر دارند.

تعریف عرض از مبدا
در ادامه می خواهیم توضیح دهیم که عرض از مبدا چیست؟ عرض از مبدأ یک عبارت است که در هندسه تحلیلی به کار میرود و عبارت است از محل برخورد تابع با محور yها. مقدارِ عددیِ عرض از مبدأ برابر است با مقدار تابع در آن نقطه. عرض از مبدا یک خط، در واقع عرض نقطه محل برخورد خط با محور عرض ها است. مثال: معادله خطی را که از دو نقطۀ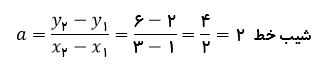 بله درسته شیب برابر است با عدد 2.
حالا برای نوشتن معادله خط به عرض از مبدا هم نیاز داریم. بیایید با استفاده از مختصات یکی از اعداد مطرح شده در سوال، معادله خط را بازنویسی کنیم و عرض از مبدا را پبدا کنیم. به طور مثال نقطه
بله درسته شیب برابر است با عدد 2.
حالا برای نوشتن معادله خط به عرض از مبدا هم نیاز داریم. بیایید با استفاده از مختصات یکی از اعداد مطرح شده در سوال، معادله خط را بازنویسی کنیم و عرض از مبدا را پبدا کنیم. به طور مثال نقطه 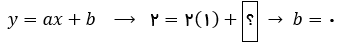 خب الان معادله ما یک مجهول دارد و جواب آن 0 ( صفر ) هست. یعنی عرض از مبدا این معادله خط برابر 0 هست.
جواب سوال معادله خط برابر است با :
خب الان معادله ما یک مجهول دارد و جواب آن 0 ( صفر ) هست. یعنی عرض از مبدا این معادله خط برابر 0 هست.
جواب سوال معادله خط برابر است با :
y=2x
نکته1: خط های مبدا گذر چیست؟
به خط هایی که عرض از مبدا آن ها صفر باشد، خط های مبدا گذر گفته می شود. مانند سوال بالانکته 2- پیدا کردن شیب خط بدون فرمول
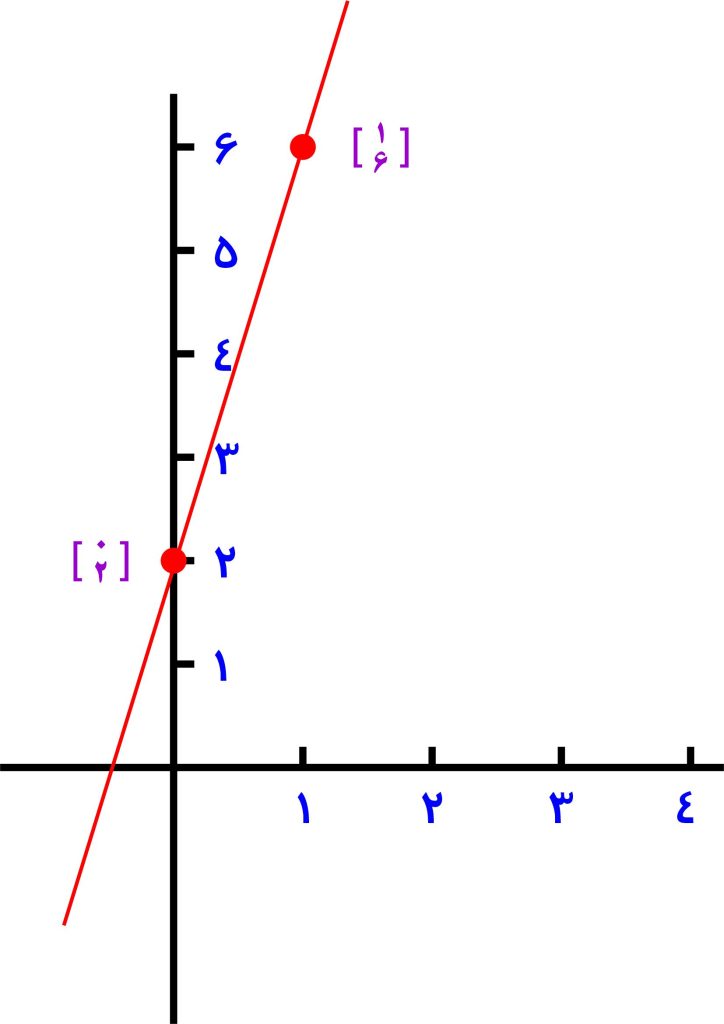
وقتی مختصات دو نقطه به شما داده می شود و در هر دو نقطه عرض نقاط، برابر حاصلضرب یک عدد در طول باشد، همان عدد می شود شیب خط. در مثال بالا عرض نقطه دوم برابر است با 1 ضربدر 2 و در نقطه دوم هم عرض برابر است با 3 ضربدر 2. یعنی عرض نقاط 2برابر طول آنها هست. 2 همان شیب خط می باشد مثال: معادلۀ خطی را که شیب آن 2 و از نقطه [2 1-] بگذرد ، را بنویسید. برای حل هر مساله ریاضی ابتدا باید ببینیم که در صورت سوال چه اطلاعاتی به ما داده شده است. در این سوال شیب ( a )= 2 و x= -1 و y = 2 حالا این اعداد را در معادله خط جا گذاری می کنیم .y = 2x + 4
خب دیدید که به همین راحتی توانستیم معادله یک خط را با استفاده از شیب و مختصات یک نقطه به دست بیاوریم.
ما در این ویدئو سعی کرده ایم یکی از مباحث پرتکرار از سری آموزش های مربوط به آموزش ریاضی نهم را به صورت جامع و کامل توضیح دهیم. مثال: معادلۀ خطی را که عرض از مبدأ آن 2 و از نقطۀ [6 1] بگذرد ، را بنویسید.برای حل اینگونه سوالات مجدد از فرمول معادله خط استفاده می کنیم و اعداد را در معادله جاگذاری می کنیم.
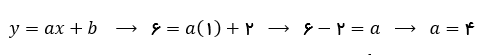
y = 4x + 2
 اگر دوست داری برای امتحان ریاضی آماده شوید و همه مسائل را به خوبی حل کنید، پیشنهاد می کنم تدریس خصوصی ریاضی مدرسان 20شو را از دست ندهید.
همانطور که در ویدئوی آموزش نوشتن معادله خط با استفاده از شیب و مختصات یک نقطه توضیح داده شد، برای نوشتن معادله خط سه حالت وجود دارد یا بهتر است بگوییم که سه نوع سوال امتحانی در مورد نوشتن معادله خط وجود دارد، که ما سعی کردیم مثال های متنوعی از هر سه حالت را داشته باشیم.
مثال: در این ویدئو به شما آموزش داده می شود که چطور معادله خط را به روش هندسی و در عرض چند دقیقه بنویسید. اول باید عرض از مبدا و شیب خط را مشخص کنید.
اگر دوست داری برای امتحان ریاضی آماده شوید و همه مسائل را به خوبی حل کنید، پیشنهاد می کنم تدریس خصوصی ریاضی مدرسان 20شو را از دست ندهید.
همانطور که در ویدئوی آموزش نوشتن معادله خط با استفاده از شیب و مختصات یک نقطه توضیح داده شد، برای نوشتن معادله خط سه حالت وجود دارد یا بهتر است بگوییم که سه نوع سوال امتحانی در مورد نوشتن معادله خط وجود دارد، که ما سعی کردیم مثال های متنوعی از هر سه حالت را داشته باشیم.
مثال: در این ویدئو به شما آموزش داده می شود که چطور معادله خط را به روش هندسی و در عرض چند دقیقه بنویسید. اول باید عرض از مبدا و شیب خط را مشخص کنید.

محصولات مرتبط
نظرات
نقد و بررسیها
اولین کسی باشید که دیدگاهی می نویسد “معادله خط شیب و عرض از مبدا آموزش ریاضی نهم” لغو پاسخ
این سایت از اکیسمت برای کاهش هرزنامه استفاده می کند. بیاموزید که چگونه اطلاعات دیدگاه های شما پردازش میشوند.


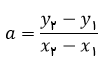






هنوز بررسیای ثبت نشده است.