آموزش قدر مطلق ریاضی نهم
آموزش قدر مطلق فصل دوم ریاضی نهم
در ابتدا به صورت ریشه ای و مفهومی به شما آموزش خواهم داد که قدر مطلق یک عدد، یعنی چه؟ من مطمئن هستم که اگر شما بتوانید مفهوم قدر مطلق را به درستی درک کنید، در حل سوالات و مثال های مربوط به قدر مطلق ریاضی نهم، مشکلی نخواهید داشت. برای تهیه پکیج ریاضی نهم با تدریس مهسا زنده دل ، کلیک کنید.
تعریف قدر مطلق در فصل دوم ریاضی نهم
یک محور اعداد را رسم کنید و عدد 2 و 2- را بر روی این محور مشخص کنید.
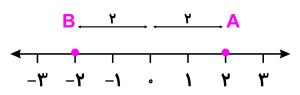
فاصله نقطه A از مبدا محور یعنی از نقطه صفر چند واحد است؟ بله درست است، فاصله نقطه A از مبدا محور 2 واحد است. همینطور فاصله نقطه B از مبدا محور 2 واحد است. توجه داشته باشید که فاصله از مبدا را با واحد نشان می دهیم و علامت نقطه در اینجا مهم نیست. همین تعریف ساده، تعریف قدر مطلق اعداد می باشد.
فاصله نقطه از مبدا محور را قدر مطلق نقطه می گویند. نماد فاصله نقطه x از مبدا ( قدر مطلق ) را با | X | نشان می دهند.
2 =| 2 | = | 2 – |
نکته 1: قدر مطلق عدد مثبت با خود عدد برابر است. یعنی اگر عدد داخل قدر مطلق یک عدد مثبت باشد، به همان صورت از قدر مطلق خارج می شود.
نکته 2: قدر مطلق عدد منفی با قرینه آن برابر است. یعنی اگر عدد داخل قدر مطلق منفی باشد، به صورت قرینه از قدر مطلق خارج می شود.

نکته 3: قدر مطلق صفر، برابر صفر است. فاصله عدد صفر از مبدا محور، صفر است.
اگر این نکات را به یاد بسپارید، از ظاهر سخت سوالات نمی ترسید. به مثال زیر توجه کنید.
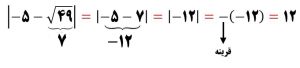
اگر این مطلب را به خوبی یاد گرفته باشید، می توانید پاسخ های خودتان را با جواب کار در کلاس صفحه 31 ریاضی نهم مقایسه کنید و اشکالات خودتان را رفع کنید.
مثال: حاصل | 8 + 10 ×(3- ) | را به دست آورید.
حل: ابتدا عبارت داخل قدر مطلق را ساده کنید و سپس با توجه به علامت جواب، آن را از قدر مطلق خارج کنید.
![]()
قضیه نامساوی مثلثی در قدر مطلق ریاضی نهم
قدر مطلق مجموع دو عدد حقیقی دلخواه، کوچکتر یا مساوی مجموع قدر مطلقهای آنهاست.

این قضیه را با یک مثال برای شما توضیح می دهم.
مثال: برقراری نامساوی مثلثی را برای عبارت | 2+1-| و |5+4| بررسی کنید.
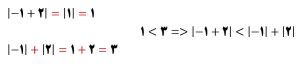
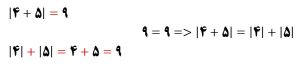
قدر مطلق تفریق دو عدد
برای به دست آوردن قدر مطلق تفریق دو عدد می توانید آن را به حاصل جمع دو عدد تبدیل کنید و از قضیه نامساوی مثلثی استفاده کنید. به این مثال توجه کنید.
![]()
قدر مطلق حاصلضرب دو عدد حقیقی
همواره به یاد داشته باشید که قدر مطلق حاصل ضرب هر دو عدد حقیقی دلخواه با حاصل ضرب قدر مطلق هر کدام از آنها برابر است.
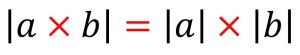
مثال: حاصل عبارت | 10 ×(3- ) | را به دست آورید.
30 = 10× 3 = | 10 |× | (3- ) | = | 10 ×(3- ) |
نکته 4: گاهی اوقات در نمونه سوال فصل دوم ریاضی نهم دیده می شود که از دانش آموز خواسته شده است حاصل عبارت قدر مطلق را ساده کنند. نیازی نیست جواب عددی همه عبارات را به دست بیائرید. در چنین سوالاتی کافی است تا علامت عبارت داخل قدرمطلق را تعیین کنید و سپس با توجه به نکات 1و 2 که در ابتدا توضیح داده شد، عبارت را ساده کنید.
مثال: عبارت | 5√ – 2 | را ساده کنید.
حل: می دانیم که 5√ از 2 بزرگتر است. پس علامت عبارت داخل قدر مطلق منفی خواهد بود. عبارات منفی از داخل قدر مطلق به صورت قرینه خارج می شوند. پس جواب می شود:
2 – 5√ = ( 5√ – 2)-
نکته 5: حاصل عبارت | a+b|- چیست؟ در چنین مواقعی ابتدا جواب عبارت داخل قدر مطلق ( هرچه که باشد ) را به دست می آوریم و سپس منفی پشت قدر مطلق را در آن تاثیر می دهیم.
قدر مطلق و ریشه دوم اعداد حقیقی
ریشۀ دوم مجذور یک عدد حقیقی برابر با قدر مطلق آن عدد شد. بنابراین برای هر عدد حقیقی دلخواه a داریم:
| a² = | a√
جمع بندی آنچه که در مورد آموزش قدر مطلق ریاضی نهم یاد گرفتیم
اگر به ویدئویی که در ابتدای صفحه وجود دارد دقت کرده باشید، 4 مثال در این ویدئو برای شما مطرح شده است که در این 4 مثال، همه آنچه را که در این قسمت از پکیج آموزش ریاضی نهم به شما یاد دادیم، عنوان شده و اگر به نکات گفته شده توجه کنید، به راحتی از عهده همه نوع سوالات مربوط به قدر مطلق بر می آیید.
خلاصه قوانین و مهمترین آنها در این عبارت خلاصه می شود. به تصویر زیر توجه کنید.
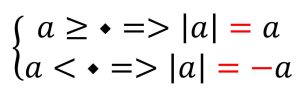











هنوز بررسیای ثبت نشده است.