مرکز تقارن و محور تقارن اشکال مختلف ریاضی هشتم

تعریف مرکز تقارن

نقطه‌ای در شکل هندسی که اگر شکل حول آن نقطه به اندازه مشخص بچرخد شکل بر خودش منطبق می شود.

انواع تقارن در اشکال هندسی

1. تقارن محوری
2. تقارن مرکزی
3. تقارن چرخشی

تعریف محور تقارن 

تقارن محوری یا محور تقارن، تقارنی ( خطی ) است که اگر شکل را از روی آن تا کنیم دو قسمت شکل بر هم منطبق می‌شود.

برای دانلود pdf مربوط به مرکز تقارن و محور تقارن اشکال مختلف در ریاضی هشتم، می توانید به پکیج آموزش ریاضی هشتم مراجعه کنید.

تعریف تقارن مرکزی

تقارن مرکزی، تقارنی است که اگر شکل را به اندازه 180درجه، حول یک نقطه بچرخانیم شکل بر خودش منطبق می شود.

تعریف تقارن چرخشی

وقتی شکل را حول یک نقطه به اندازه 180درجه یا کمتر (وحتی بیشتر) در جهت عقربه های ساعت می چرخانیم و شکل روی خودش می افتد می گوییم شکل تقارن چرخشی دارد.

تعریف دوران در اشکال هندسی

چرخش یک شکل حول یک نقطه را دوران می گویند.

انواع دوران

1. دوران 90درجه
2. دوران 180درجه

انواع قرینه

1. قرینه نسبت به یک خط (خط تقارن عمود ی، خط تقارن افقی )
2. قرینه نسبت به یک نقطه

نکات مهم درباره تقارن

تقارن محوری: درتقارن محوری قرینه یک نقطه را نسبت به یک خط بدست می آوریم.

محور تقارن خطی است که قرینه هر نقطه ازشکل نسبت به آن برخود شکل منطبق می شود. یا خطی است که شکل را به دو قسمت مساوی تقسیم می کند.

تقارن مرکزی: در تقارن مرکزی قرینه یک شکل را نسبت به یک نقطه بدست می آوریم که آن نقطه مرکز تقارن شکل است.

مرکز تقارن نقطه ای است که قرینه هر نقطه از شکل نسبت به آن برخود شکل منطبق می شود.

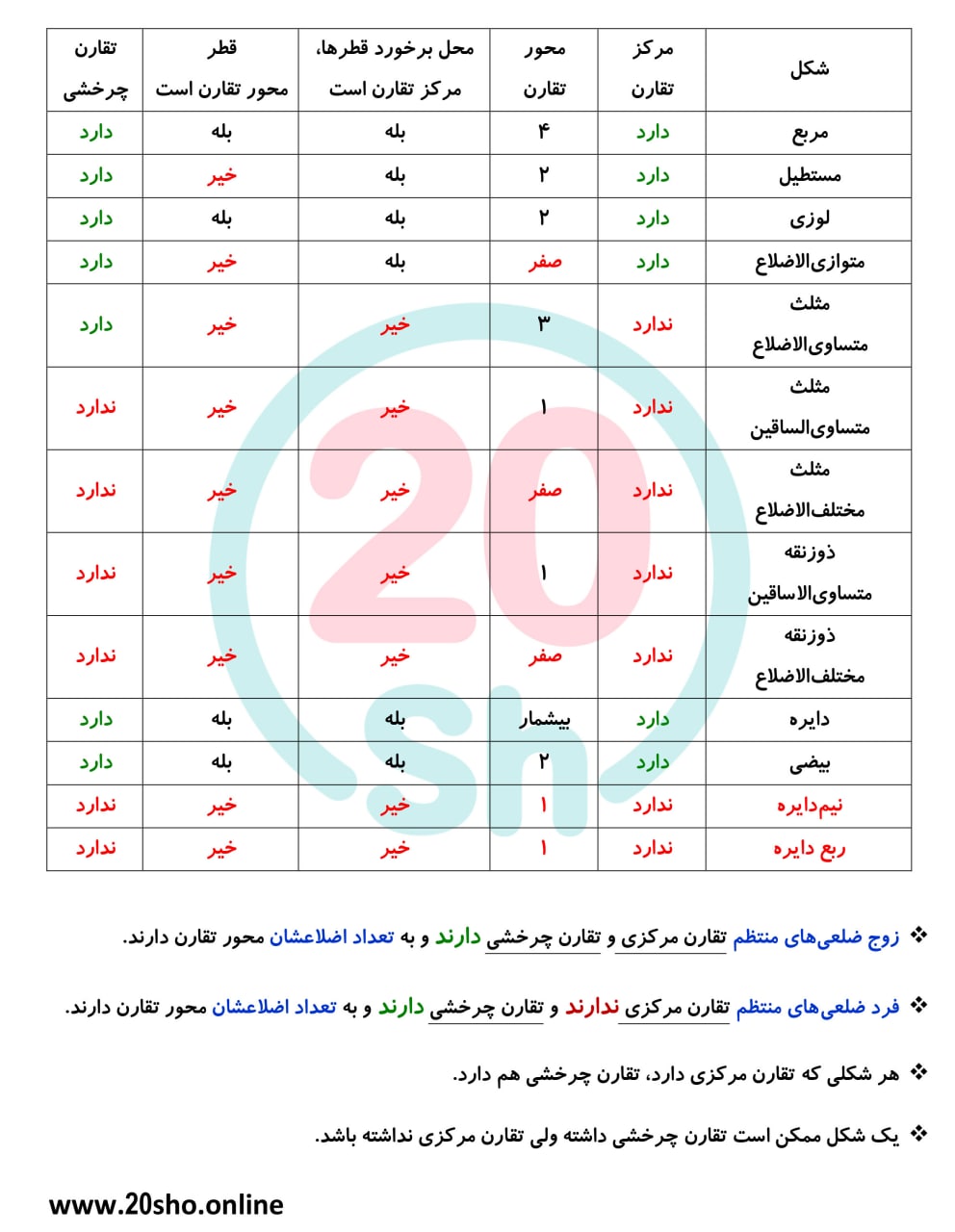
• مربع 4 تا محور تقارن دارد.
• مستطیل دو تا محور تقارن دارد.
• لوزی  2 تا محور تقارن دارد.
• متوازی الاضلاع محور تقارن ندارد.
• دایره بی شمار محور تقارن دارد.
• مثلث متساوی الاضلاع 3 تا محور تقارن دارد.
• مثلث متساوی الساقین یک محور تقارن دارد.

ذوزنقه متساوی الساقین یک محور تقارن دارد.

الف) نقطه: یک مرکز تقارن دارد و آن خودش است،  وبی شمار محور تقارن دارد.

ب) خط: بی شمار مرکز تقارن دارد، کلیه نقاطی که روی خط قرار دارند. بی شمار محور تقارن دارد. خطوطی که بر این نقاط می گذرند.

ج) n ضلعی منتظم: n محور تقارن دارد، اگر  n زوج باشد یک مرکز تقارن دارد و اگر n فرد باشد مرکز تقارن ندارد.

د) نیم خط: نیم خط مرکز تقارن ندارد ولی یک محور تقارن دارد.

ه) پاره خط: دو محور تقارن عمود برهم دارد، یکی عمود منصف آن و دیگری خطی است که پاره خط جزیی از آن است و یک مرکز تقارن دارد.

• ذوزنقه ها درحالت کلی محور تقارن ندارند.
• یک مثلث در حالت کلی محور تقارن و مرکزتقارن ندارد.
• مثلث متساوی الساقین مرکز تقارن ندارد.
• مثلث متساوی الاضلاع مرکز تقارن ندارد.
• متوازی الاضلاع تنها شکل هندسی منظمی که مرکز تقارن دارد ولی محور ندارد.

با یادگیری درست محور تقارن و مرکز تقارن باید بتوانید به این سوالات پاسخ دهید:

1. مرکز تقارن چیست؟
2. چند شکل نام ببرید که تقارن چرخشی دارند
3. شکلی که مرکز تقارن دارد ولی محور تقارن ندارد
4. شکلی که مرکز تقارن دارد ولی خط تقارن ندارد
5. مثلث متساوی الاضلاع مرکز تقارن دارد؟
6. کدام شکل مرکز تقارن دارد ولی محور تقارن ندارد
7. ذوزنقه متساوی الساقین مرکز تقارن دارد؟
8. تقارن مرکزی چیست؟
9. خط تقارن اشکال هندسی
10. کدام شکل محور تقارن ندارد ولی مرکز تقارن دارد؟
11. مثلث متساوی الساقین چند محور تقارن دارد؟
12. مربع چند خط تقارن دارد؟
13. لوزی چند محور تقارن دارد؟
14. شکل هایی که تقارن چرخشی دارند؟
15. کدام شکل مرکز تقارن ندارد؟
16. شکلی که محور تقارن دارد ولی مرکز تقارن ندارد چه نام دارد؟
17. چه شکل هایی مرکز تقارن دارند؟
18. چه شکل هایی تقارن چرخشی دارند؟
19. چند شکل که تقارن چرخشی دارند؟
20. سه شکل که تقارن چرخشی دارند؟
21. تقارن چرخشی چیست؟
22. متوازی الاضلاع تقارن چرخشی دارد؟
23. مثلث متساوی الساقین مرکز تقارن دارد؟
24. متوازی الاضلاع چند خط تقارن دارد؟
25. هر شکل هندسی حداکثر چند مرکز تقارن دارد؟
26. کدام شکل تقارن چرخشی ندارد؟