آموزش مجموعه ها و احتمال ریاضی نهم
آموزش احتمال درس چهارم فصل اول ریاضی نهم
در مبحث احتمال ریاضی نهم می خواهیم از آموزش مجموعه ها ریاضی نهم کمک بگیریم. می پرسید رابطه بین مجموعه ها و احتمال چیست؟ باید مجموعه ها را خوب یاد گرفته باشید تا بتوانید فضای نمونه، پیشامد و احتمال را به زبان مجموعه ها بنویسید. به طور مثال در پرتاب سکه و تاس باید بتوانید مجموعه فضای نمونه و پیشامد را بنویسید. برای یاد گرفتن کلیه حالت های احتمال در پرتاب سکه و تاس و دیگر مثال ها تا پایان با ما همراه باشید. یکی از مبحث های مهم پکیج آموزش ریاضی نهم را خواهیم داشت.
تعریف احتمال و پیشامد با استفاده از مجموعه ها
در احتمال، پیشامد یعنی اتفاق. یعنی چی؟ تصور کنید یک تاس را پرتاب می کنید. هر بار ممکن است یکی از اعداد 1 تا 6 رو بیاید. به هر کدام از این اتفاق ها و رو شدن هر یک از اعداد یک پیشامد گفته می شود و تعداد اعضای آن را با مجموعه نمایش می دهند.
احتمال رو شدن هر یک از اعداد 1 تا 6 یعنی احتمال پیشامد را با P(A) نمایش می دهند.
در پرتاب یک تاس احتمال پیشامد عدد 3 را با P(3) نشان می دهند.
فرمول احتمال یک پیشامد
در آموزش ریاضی هشتم در مورد احتمال اتفاق افتادن یک پیشامد یاد گرفته اید. برای یادآوری فرمول آن را مجدد با هم مرور می کنیم. احتمال یک پیشامد برابر است با تعداد اعضای مجموعه پیشامد به تعداد اعضای مجموعه فضای نمونه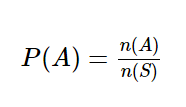
فضای نمونه در احتمال ریاضی نهم
مجموعه تمام حالت های ممکن و مجموعه تمام پیشامدها را فضای نمونه می گویند و آن را به S نمایش می دهند. در فرمول بالا احتمال پیشامد عدد 3 برابر است با تعداد اعضای مجموعه پیشامد 3 تقسیم بر تعداد اعضای مجموعه فضای نمونه.
نکته 1: با توجه به نکاتی که گفته شد، مشخص است که هر پیشامد، یک زیرمجموعه از فضای نمونه است. چرا که جمع همه پیشامدها، فضای نمونه را تشکیل می دهد. پس تک تک پیشامدها عضو فضای نمونه هستند.
مثال هایی در مورد احتمال و فضای نمونه
1- تاسی را یکبار پرتاب می کنیم. احتمال اینکه عدد فرد بیاید، چقدر است؟
حل: اول مجموعه فضای نمونه ( تمامی حالت های ممکن در پرتاب تاس ) را بررسی می کنیم و آن را با S نشان می دهیم.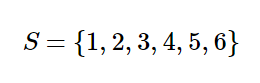
مجموعه پیشامد عدد فرد در پرتاب تاس را هم با A نشان می دهیم.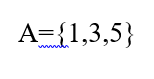
فرمول احتمال پیشامد که یادتان است. از همان فرمول استفاده می کنیم و اعداد را در فرمول جاگذاری می کنیم. 3 تعداد اعضای مجموعه پیشامد و 6 تعداد اعضای مجموعه فضای نمونه است: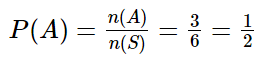
نمودار ون پرتاب تاس ( فضای نمونه و پیشامد پرتاب تاس )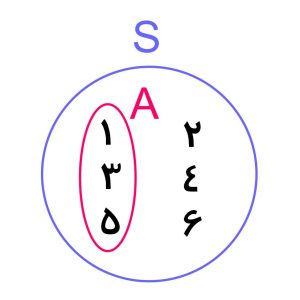
2- در پرتاب یک سکه و یک تاس به صورت همزمان،چقدر احتمال دارد سکه رو و تاس زوج بیاید؟
حل: برای پرتاب سکه دو حالت رو و پشت وجود دارد و برای پرتاب تاس 6 حالت از 1 تا 6 وجود دارد. ترکیب این حالت ها فضای نمونه پرتاب سکه و تاس به صورت همزمان را تشکیل می دهد.
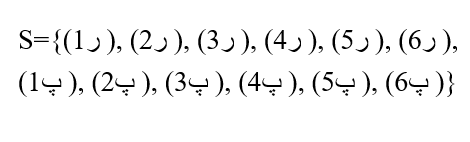
تعداد اعضای مجموعه پیشامد ( سکه رو و تاس زوج ) را هم با A نشان می دهیم. حالت های نامطلوب را از فضای نمونه حذف می کنیم. برای راحتی کار هر پیشامدی که سکه پشت هست را حذف کنید. تعداد حالت های باقی مانده مانند تصویر زیر به 6 حالت کاهش پیدا می کند.
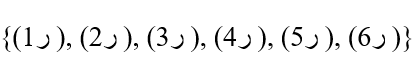
از این 6 حالت هم تعداد نامطلوب باقی مانده را حذف می کنیم. یعنی تمامی پیشامدهایی که سکه رو و تاس فرد است را حذف می کنیم.
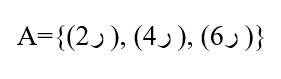
تعداد مجموعه فضای نمونه برابر12 = n(S) و تعداد اعضای پیشامد A برابر 3 = n(A) است. با جاگذاری در فرمول جواب به راحتی بدست می آید.
P(A)=n(A)/n(S)=3/12
پرتاب متوالی تاس در احتمال ریاضی نهم
ممکن است طراح سوال به این حالت سوال را طرح کند که یک تاس را دوبار پرتاب می کنیم یا 2 تاس را به صورت همزمان پرتاب می کنیم. در این حالت اگر بخواهید فضای نمونه را یک به یک بنویسید وقت شما در سر جلسه امتحان گرفته می شود. یک روش تستی برای به دست آوردن تعداد اعضای مجموعه فضای نمونه یعنی n(S) این است که تعداد حالت های هر کدام را در تعداد حالت های دیگری ضرب کنید. برای تاس اول 6 پیشامد و برای تاس دوم هم 6 پیشامد و حالت وجود دارد. 6*6= 36 پس تعداد 36 = n(S)
3- یک تاس را دوبار پرتاب کنید، احتمال اینکه هر دوبار مضرب 3 بیاید چه قدر است؟
حل: ابتدا تعداد پیشامدهای مضرب 3 را مشخص کنید. در پرتاب تاس عدد 3 و 6 مضرب عدد 3 هستند. پس می توانیم مجموعه پیشامد A را به صورت زوج مرتب که مولفه اول مربوط به پرتاب اول و مولفه دوم مربوط به پرتاب دوم است، بنویسیم.
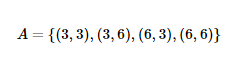
مشخص است که 4 = n(A) است و 36 = n(S). براحتی از طریق فرمول احتمال ریاضی نهم می توانیم جواب صحیح را بدست بیاویرم.
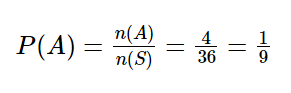
تعداد حالات نشستن اعضای کابینه دور یک میز
یکی از سوالاتی که می توان با مبحث مجموعه ها و احتمال آن را حل کرد، احتمال نشستن دور میز است. به این سوال دقت کنید و جواب آن را در این ویدئو ببینید.
سوال: در یک جلسه بین مدیر، منشی و 4 کارمند، دور یک میز گرد، احتمال اینکه مدیر روبروی منشی بنشیند، چقدر است؟










بحرانی –
عالی
Edris (خریدار محصول) –
خیلی ممنون از تدریستون
مهسا زنده دل –
سلام
خوشحالم که تدریس مجموعه ها و احتمال در ریاضی نهم مورد توجه شما قرار گرفته.
حسام نیامی –
واقعا عالی
مهسا زنده دل –
ممنون آقای نیامی عزیز
خوشحالم که این آموزش در خصوص درس احتمال ریاضی نهم مورد پسند شما قرار گرفته