آشنایی با اثبات در هندسه ریاضی نهم

در درس آشنایی با اثبات در هندسه ریاضی نهم، ( نمونه ویدئوی رایگان از پکیج آموزش ریاضی نهم ) که مربوط به درس دوم فصل سوم است با دو مفهوم اساسی آشنا می شویم. با درک عمیق این مفاهیم شما می توانید بر درس آشنایی با اثبات در هندسه تسلط کامل پیدا کنید و هر نوع نمونه سوال فصل سوم ریاضی نهم را به راحتی حل کنید.

1. آشنایی با فرض و حکم یک مسئله و اینکه فرض و حکم چه چیزهایی هستند؟
2. تعمیم نتیجۀ یک استدلال چیست و چه کاربردی دارد؟

فرض و حکم در آشنایی با اثبات در هندسه نهم

در حل هر مساله اولین قدم این است که فرض و حکم مساله را به درستی تشخیص دهید. حال با هم بررسی می کنیم که فرض و حکم مساله چیست؟

تعریف فرض در آشنایی با اثبات در هندسه نهم

فرض یک مساله همان اطلاعاتی است که در صورت مساله مطرح شده و به ما کمک می کند تا مساله را با آن اطلاعات حل کنیم.

تعریف حکم در آشنایی با اثبات در هندسه نهم

هر مساله ای که مطرح می شود، خواسته ای دارد که باید با توجه به فرض مساله و اطلاعات داده شده، آن را به دست بیاوریم. در یک کلام می توان گفت که حکم مساله، همان خواسته ی مساله از ما است.

مثالی از تشخیص فرض و حکم مساله

در مسئلۀ زیر، فرض و حکم را مشخص کنید.

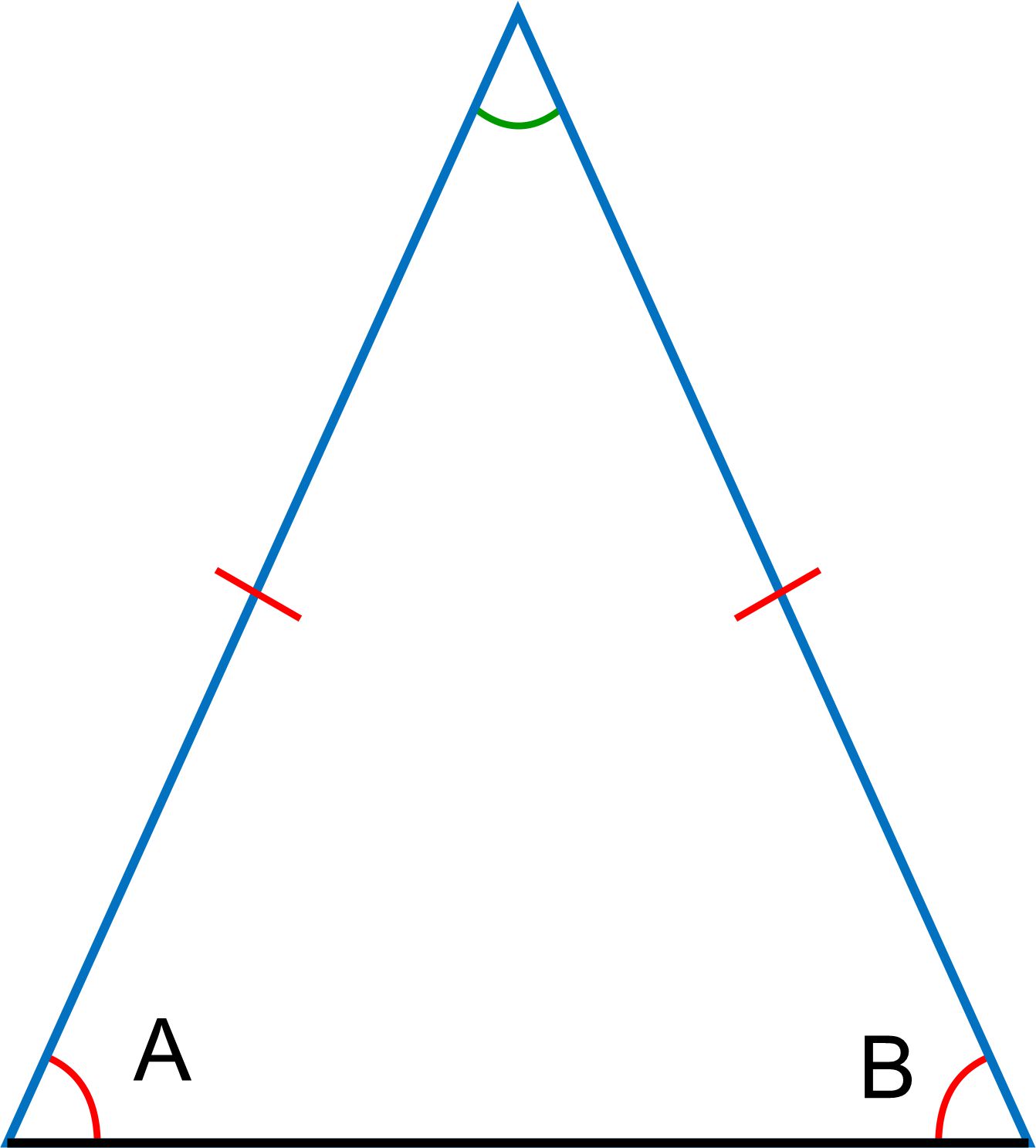
مثال 1: در شکل زیر زاویه A و B زوایای قاعده یک مثلث متساوی الساقین هستند. ثابت کنید که زاویه A و B  با هم برابر هستند.

مثال 2: ثابت کنید در هر مثلث مجموع زوایای داخلی برابر با 180 درجه است.

تعمیم نتیجه در آشنایی با اثبات در هندسه نهم

تعمیم نتیجه حاصل از استدلال به مثال ها و مسائل مشابه، قدم بعدی در درس دوم فصل سوم ریاضی نهم، آشنایی با اثبات در هندسه است. در بسیاری مسائل مشابه می توانیم از استدلال ها و نتایجی که به دست آورده ایم، استفاده کنیم. چرا که در استدلال این مسائل از فرض ها و ویژگی های مشابه استفاده شده و در مساله دیگر نیز به همین فرض ها نیاز داریم. پس می توانیم نتایج آن را تعمیم دهیم.

مثال 3: در شکل زیر، مثلث ABC متساوی‌الاضلاع است. AD نیمساز زاویۀ A است. ثابت کنید AD میانه است. آیا می‌توانیم بدون اینکه اثبات را بازنویسی کنیم، نتیجه بگیریم نیمساز‌های زوایای B و C نیز میانه‌اند؟

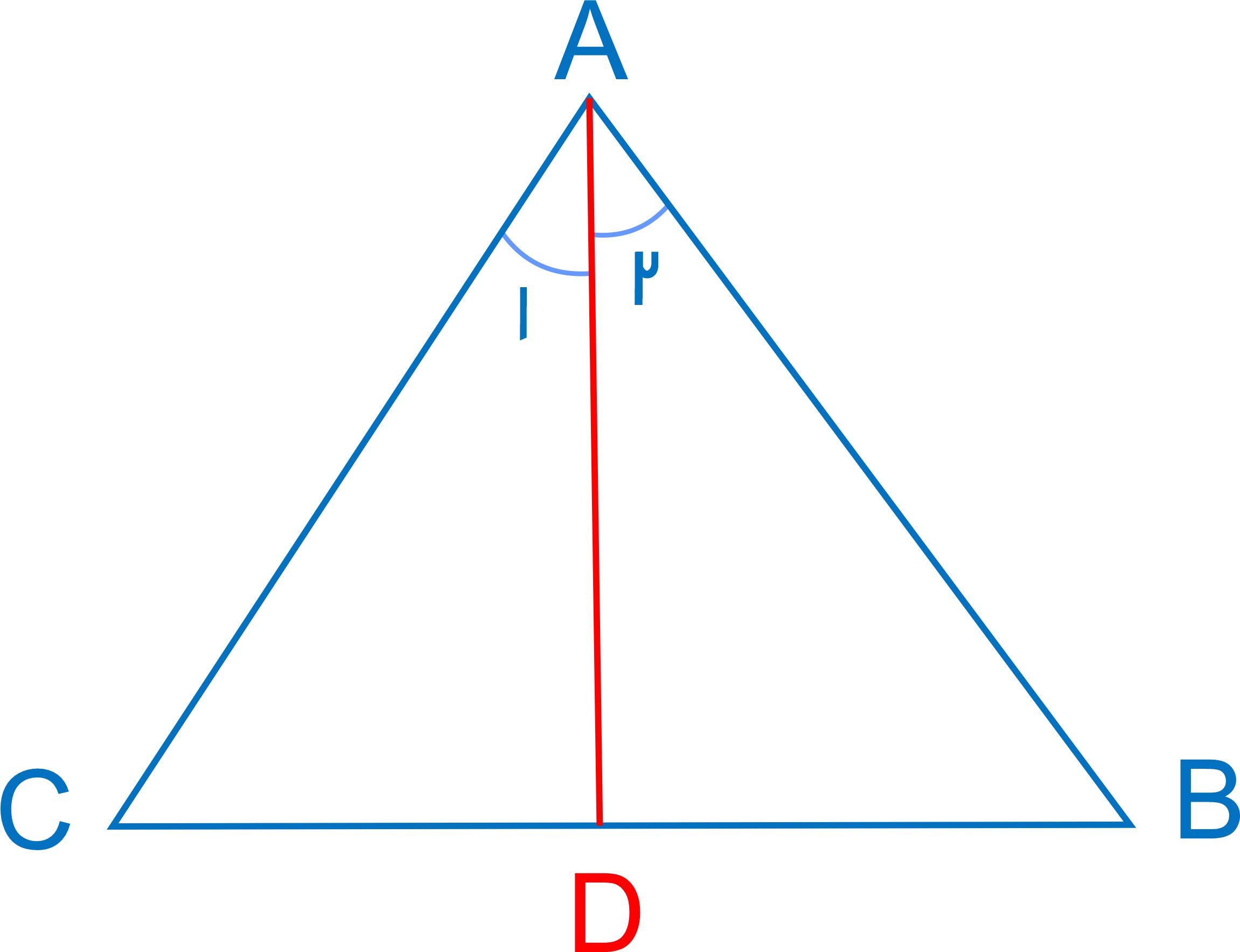
ابتدا باید ثابت کنیم که مثلث‌های ABD و ACD هم‌نهشت هستند.

بنابراین BD=CD. در نتیجه AD میانه است.در قسمت دیگر سوال پرسیده شده است که آیا می‌توانیم بدون بازنویسی اثبات، نتیجه بگیریم نیمساز‌های زوایای B و C نیز میانه‌اند؟

برای اثبات میانه بودن AD تنها از برابری اضلاع AB و AC و برابری زوایای A1 و A2 استفاده کردیم. نیمساز هم که در هر صورتی مشترک است، از آنجاییکه تمام اضلاع مثلث متساوی الاضلاع با هم برابرند، بنابراین اگر نیمساز زوایای دیگر را نیز در نظر بگیریم می‌توانیم میانه بودن آن‌ها را نتیجه گیری کنیم.

بررسی اثبات‌های معتبر و نامعتبر در اثبات در هندسه نهم

دقت داشته باشید که مسائلی وجود دارد که می تواند باعث نامعتبری اثبات یا کلاً اثبات اشتباه شود. اگر این موارد را بشناسید به این دلایل و فرضیات غلط در اثبات حکم تکیه نخواهید کرد. چند مورد را با هم بررسی می کنیم.

اثبات با اندازه‌گیری ابعاد یک شکل

اندازه‌گیری ابعاد یک شکل، نمی تواند به عنوان فرضیات آن مساله مورد توجه و استدلال قرار گیرد و در نتیجه نمی توان با تکیه بر آنها، حکم یک مسئله را ثابت کرد.

به طور مثال فرض کنید از ما خواسته شده که ثابت کنیم زاویه های قاعده یک مثلث متساوی الساقین، با هم برابر هستند. برای اثبات این حکم نمی توانیم چند مثلث متساوی الساقین رسم کنید و از طریق اندازه گیری زوایای قاعده آن، حکم مساله را ثابت کنید. چرا که در این روش احتمال اشتباه در اندازه گیری بسیار بالا است.

اثبات برای یک حالت خاص

در مساله ای خواسته شده است که ثابت کنیم در هر مثلث، اندازۀ زوایای خارجی برابر است با مجموع دو زاویۀ داخلی غیر مجاور.

یک نمونه اثبات اشتباه برای این نوع سوالات این است که مثلث متساوی‌الاضلاع ABC را در نظر بگیریم:

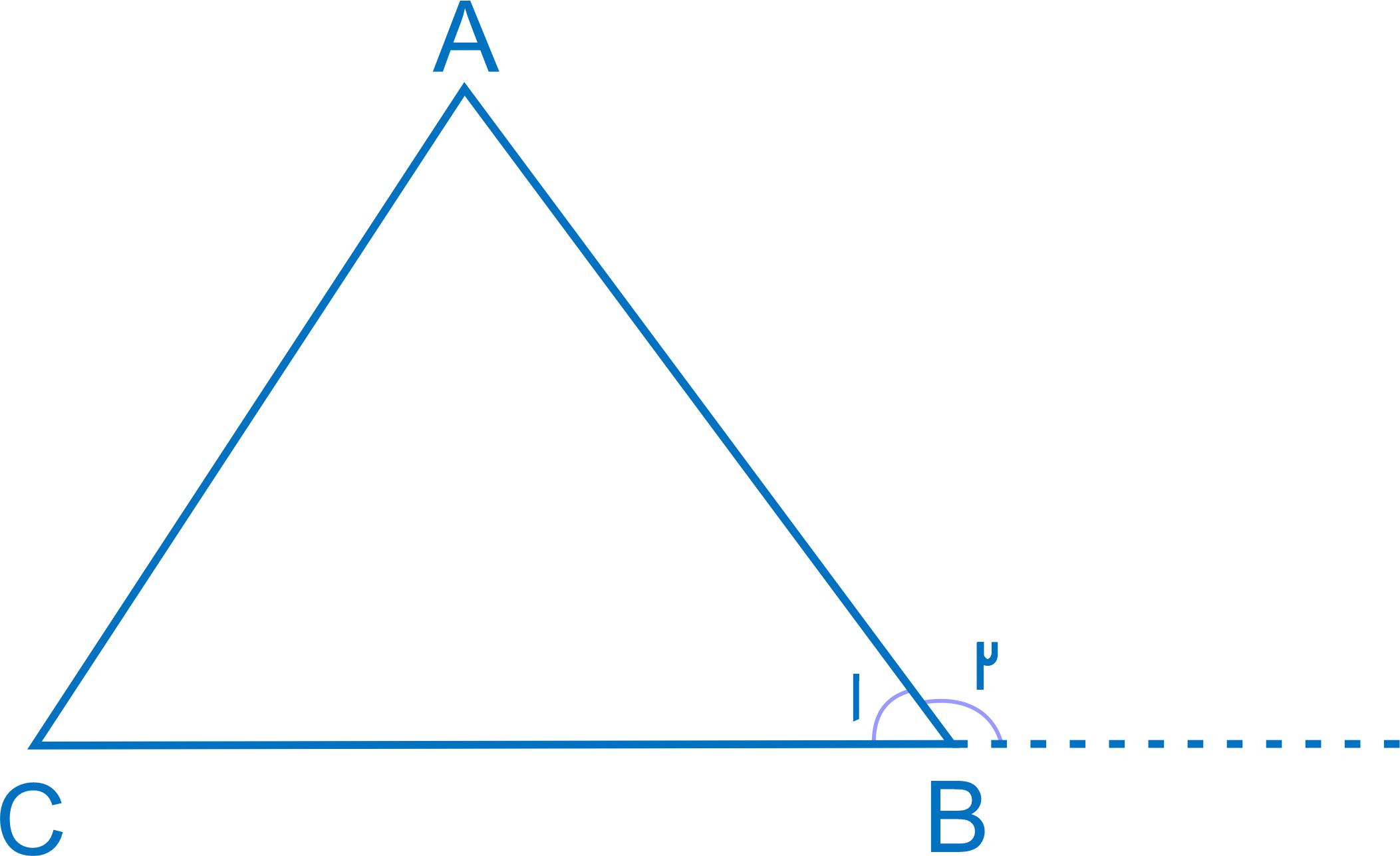
مشخص است که در هر مثلث متساوی الاضلاع، اندازه هر یک از زوایای داخلی 60 درجه می باشد. بنابراین زاویۀ B1 برابر با 60 درجه بوده و زاویۀ B2 برابر با 120 درجه است. ( چون مجموع هر زاویه داخلی و خارجی برابر با 180 درجه است ) از آنجاییکه اندازۀ A و C هم هر کدام برابر با 60 درجه است، پس داریم:

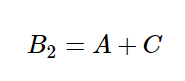
اشتباه نکنید. این یک اثبات کاملاً اشتباه است. چرا که در مساله از ما خواسته شده است که این حکم را برای همه نوع مثلث ( هر مثلثی ) اثبات کنیم، در حالیکه با این روش فقط برای مثلث متساوی الاضلاع اثبات می شود.

یک مثال دیگر از مبحث آشنایی با اثبات در هندسه نهم