آموزش توان صحیح ریاضی نهم فصل 4
همه ما قبلاً به توان رسوندن اعداد را یاد گرفته ایم و به خوبی با مفهوم توان آشنا هستیم. در درس اول فصل چهارم مبحث توان صحیح ریاضی نهم مطرح شده است. تفاوت این آموزش با توان های طبیعی که قبلاً یاد گرفته ایم در این است که می آموزیم چطور اعداد را به توان صحیح ( ممکن است توان عدد منفی باشد ) برسانیم. پیشنهاد می کنم ضمن مطالعه ی متن این صفحه و حل مثال های مطرح شده، ویدئوی آموزش توان صحیح ریاضی نهم که قسمتی از پکیج ریاضی نهم است، را تماشا کنید تا این درس را به طور کامل یاد بگیرید.
چگونه اعداد را به توان منفی برسانیم؟
خب این یک سوال اساسی هست که مبنای درس اول فصل چهارم ریاضی نهم نیز هست. وقتی با عبارت ![]() روبرو می شوید، تکلیف مشخص است یعنی 4 بار باید 5 را در خودش ضرب کنید.
روبرو می شوید، تکلیف مشخص است یعنی 4 بار باید 5 را در خودش ضرب کنید.
ولی وقتی توان عدد، منفی باشد تکلیف چیست. ![]() برای اینکه 5 را 4- بار به توان برسانیم راه حل چیست؟
برای اینکه 5 را 4- بار به توان برسانیم راه حل چیست؟
قانون اول توان منفی ( توان صحیح ) اعداد
اگر n یک عدد طبیعی و a عددی مخالف صفر باشد، در مورد توان منفی می توانید این قانون کلی را به کار ببرید. یعنی پایه عدد تواندار را معکوس کنید و آن را به توان مثبت برسانید.
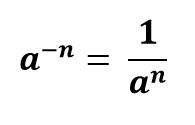
چند مثال از توان منفی ریاضی نهم
مثال 1: حاصل عبارت 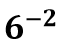 را بنویسید.
را بنویسید.
حل: برای حل این سوال، ابتدا پایه را معکوس کرده و مخرج را به توان مثبت برسانید. 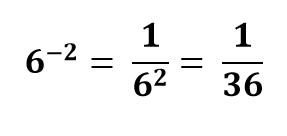
مثال بعدی از توان منفی یک کسر است. با دانستن قانون کلی توان صحیح ریاضی نهم، فرقی نمی کند پایه تواندار شما عدد طبیعی باشد یا یک کسر باشد.
مثال 2: عبارت 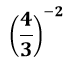 را ساده کنید.
را ساده کنید.
حل: قانون کلی را در نظر بگیرید. فرقی نمی کند پایه عدد طبیعی باشد یا عبارت گویا ( کسری ) . برای حل این سوال با همان قانون پیش می رویم.
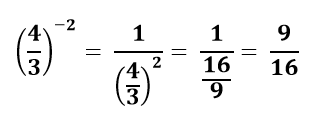
قانون دوم توان منفی اعداد ریاضی نهم
وقتی پایه به جای یک عدد صحیح یا طبیعی، یک کسر باشد و به توان منفی رسیده باشد، هم می توانید از قانون اول تبعیت کنید یا یک راه میانبر بزنید و از این قانون پیروی کنید.
اگر n یک عدد طبیعی و a عددی مخالف صفر باشد، در مورد توان منفی می توانید این قانون کلی را به کار ببرید.
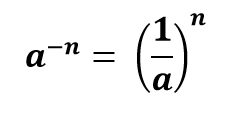
حال اگر بخواهید مثال 2 را با همین روش محاسبه کنید، پاسخ به این صورت خواهد بود.
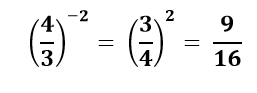
در ادامه مبحث توان صحیح ریاضی نهم، به بیان چند رابطه و قانون کلی در مورد اعداد تواندار با توان صحیح می پردازیم که اگر آنها را به خوبی درک کنید و بخاطر بسپارید، در حل هیچ کدام از نمونه سوال فصل چهارم ریاضی نهم با مشکل روبرو نخواهید شد.
ضرب اعداد با توان صحیح
اگر m و n دو عدد صحیح باشند و a یک عدد مخالف صفر باشد، آنگاه رابطه زیر همواره برقرار خواهد بود.
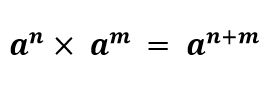
حال اگر یکی از توان ها منفی باشد، در کلیت این قانون هیچ خللی ایجاد نمی شود و با همین فرمول می توان آن را حل کرد.
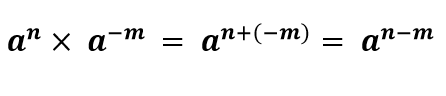
مثال از ضرب اعداد با توان صحیح
مثال 3: حاصل عبارت ![]() را به دست آورید.
را به دست آورید.
برای حل این سوال قانون ضرب اعداد با توان صحیح را به یاد بیاورید.
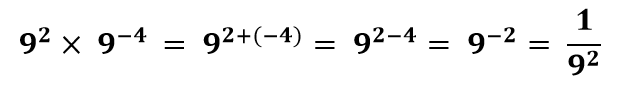
مثال 4: حاصل عبارت ![]() را به دست آورید.
را به دست آورید.
از ظاهر سوال نترسید. قانون برای همه نوع اعداد یکی است. فرقی نمی کند پایه شما عدد صحیح باشد یا گویا. در این مثال یک عبارت گویا با توان منفی داریم که باید آن را ساده کنید. با استفاده از قانون ضرب اعداد با توان صحیح به راحتی به پاسخ صحیح می رسید.
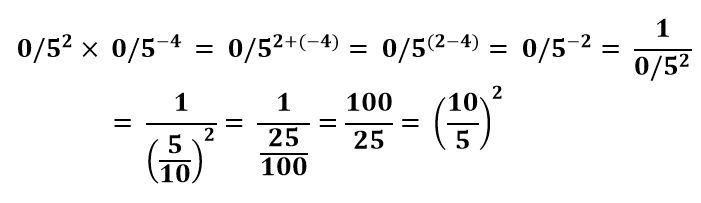
تقسیم اعداد با توان صحیح
اگر m و n دو عدد صحیح باشند و a یک عدد مخالف صفر باشد، آنگاه رابطه زیر همواره برقرار خواهد بود.
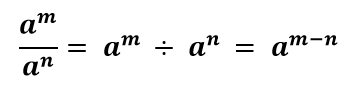
مثال از تقسیم اعداد با توان صحیح
مثال 5: حاصل عبارت ![]() را به دست آورید.
را به دست آورید.
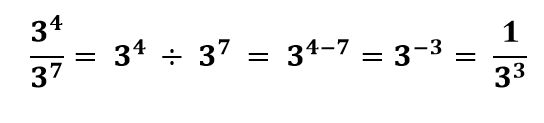
تقسیم اعداد با پایه های نابرابر و توان های مساوی
یکی دیگر از قوانینی که در درس توان صحیح ریاضی نهم به آن می پردازیم و بسیاری از مسائل را با توجه به آن حل می کنیم همین قانون است که فرمول آن به این شکل است.
اگر m یک عدد صحیح و a و b دو عدد دلخواه و مخالف صفر باشند، آنگاه داریم:
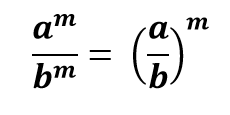
ضرب اعداد با پایه های نابرابر و توان های مساوی
اگر m یک عدد صحیح و a و b دو عدد دلخواه و مخالف صفر باشند، آنگاه داریم:
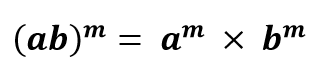
مثال 6: حاصل عبارت 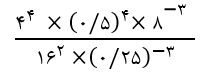 را به دست آورید.
را به دست آورید.
برای حل این سوال، ابتدا عبارت های داده شده را در حد امکان ساده می کنیم.
برای درک بهتر روش حل این سوال، می توانید ویدئوی آموزشی توان صحیح ریاضی نهم که در ابتدای همین صفحه وجود دارد را تماشا کنید. دقت داشته باشید که در این سوال از همه قوانینی که در این درس یاد گرفتیم استفاده شده است.
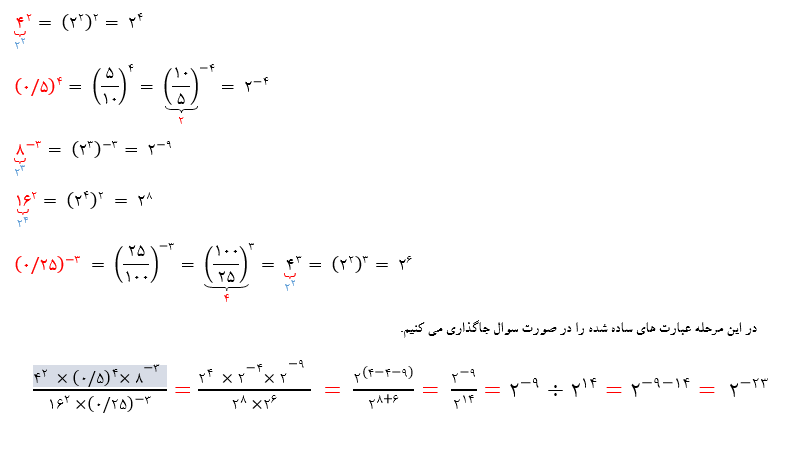
جمع بندی قوانین توان صحیح درس دوم فصل چهارم ریاضی نهم
اگر همین چند قانون کلی را در مبحث توان صحیح ریاضی نهم یاد بگیرید، از عهده همه سوالات امتحانی برخواهید آمد. فقط کافی است که این قوانین را به خاطر بسپارید و بدانید از هر کدام در کجا باید استفاده کنید.
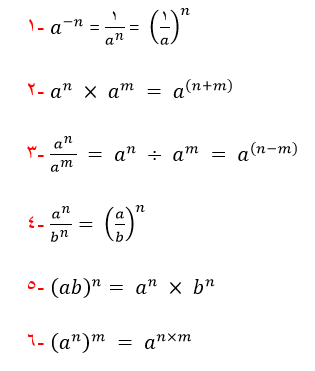










هنوز بررسیای ثبت نشده است.