مهسا زنده دل
درباره مدرس دارای مدرک کارشناسی ارشد هوش مصنوعی و ۸ سال سابقه تدریس ریاضی و تیزهوشان از مقطع ششم تا نهم به صورت حضوری و آنلاین. مبتکر آموزش به شیوه خلاقانه با...
مشاهده بیشتراجتماع، اشتراک و تفاضل مجموعه ها
آموزش اجتماع، اشتراک و تفاضل مجموعه ها درس سوم فصل اول ریاضی نهم
ما قبلاً با ویدئوی معرفی مجموعه ها ریاضی نهم به طور مفصل در مورد نکات مهم نوشتن مجموعه ها و درس مجموعه ها آشنا شدیم. در این ویدئوی آموزشی می خواهیم با مفهوم اجتماع، اشتراک و تفاضل مجموعه ها آشنا شویم. ضمن اینکه این آموزش قسمتی از پکیج ریاضی نهم نیز می باشد.
اجتماع مجموعه ها ریاضی نهم
فرض کنید شما دو مجموعه به نام A و B دارید که اعضای هر کدام مشخص است. منظور از اجتماع دو مجموعه این است که اعضای هر دو مجموعه A و B را بدون تکرار اعضا در یک مجموعه جمع کنیم. به عبارتی اعضای اجتماع دو مجموعه حداقل عضو یکی از مجموعه های A یا B می باشد. به کلمه ” یا ” خوب دقت کنید.
نمایش اجتماع دو مجموعه
برای نشان دادن اجتماع دو مجموعه از علامت A∪B استفاده می شود و برای نشان دادن آن به زبان ریاضی به این صورت می نویسیم.
A∪B={x|x∈A یا x∈B}
نکته 1:از قبل یاد گرفته اید که مجموعه ها دارای خاصیت جابجایی هستند. یعنی با جابجایی اعضای مجموعه، مجموعه جدیدی به دست نمی آید. پس در نوشتن اجتماع دو مجموعه هم فرقی نمی کند ابتدا اعضای کدام مجموعه نوشته شود.
A∪B = B∪A
نمونه سوال اجتماع و اشتراک مجموعه ها
مثال اجتماع دو مجموعه
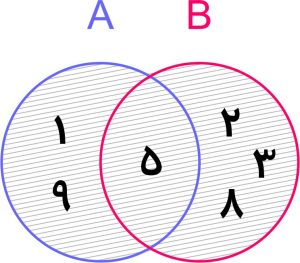
1- اگر A={1,5,9} و B={2,3,5,8} باشد، A∪B را به دست آورده و نمودار وِن آن را رسم کنید.
حل: دقت کنید که در بالا اشاره کردیم که برای نوشتن اجتماع دو مجموعه، اعضای تکراری را حذف می کنیم و بدون تکرار اعضا می نویسیم. یعنی 3 و 8 که در هر دو مجموعه تکرار شده اند را فقط یکبار در اجتماع دو مجموعه می نویسیم و بقیه اعضای تکراری را هم در کنار هم جمع می کنیم. قسمت هاشور خورده در نمودار ون هم اجتماع دو مجموعه را نشان می دهد.
A∪B={1,5,9,2,3,8}
مجموعه شمارنده های طبیعی عدد 16برابر است با: A={1,2,4,8،16}
B={1,3,7,21}:مجموعه شمارنده های طبیعی عدد 21برابر است با
حالت خاص اجتماع دو مجموعه
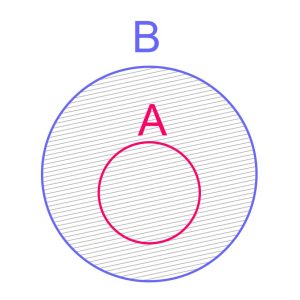
فرض کنید برای دو مجموعۀ A و B به این شکل داشته باشیم A⊆B. آنگاه اجتماع دو مجموعه A و B چه خواهد شد؟
یاد گرفتیم که در اجتماع دو مجموعه، 2 شرط مهم را باید رعایت کنیم.
شرط اول اجتماع دو مجموعه این است که اعضای اجتماع دو مجموعه حداقل عضو یکی از مجموعه ها باشند.
شرط دوم اجتماع دو مجموعه این است که اعضا باید غیرتکراری باشند.
از صورت سوال مشخص است که همه اعضای A در B وجود دارند. بنابراین اگر بخواهیم اعضای دو مجموعه را با هم جمع کنیم اعضای تکراری را حذف می کنیم که همان اعضای مجموعه A خواهند بود. بنابراین اعضای باقی مانده همان اعضای مجموعه B می باشند. پس جواب به این صورت است: A∪B=B
نمودار ون برای این حالت خاص از اجتماع مجموعه ها که یکی از مجموعه ها زیرمجموعه دیگری می باشد، به این شکل است:
اشتراک مجموعه ها ریاضی نهم
شما دو مجموعه به نام A و B دارید که اعضای هر کدام مشخص است. منظور از اشتراک دو مجموعه این است که اعضایی از هر دو مجموعه A و B را که هم در A و هم در B وجود دارند را در یک مجموعه جمع کنیم. مشخص است که اعضای مشترک که در هر دو مجموعه تکرار شده اند، مد نظر می باشد. دقت کنید که بر عکس اجتماع مجموعه ها از حرف ” و ” استفاده شده است.
نمایش اشتراک دو مجموعه
A∩B={x|x∈A و x∈B}
نکته 2: اگر با مفهوم اشتراک دو مجموعه به خوبی آشنا شده باشید متوجه می شوید که اشتراک هر دو مجموعه A و B، زیرمجموعه هر یک از مجوعه های A و B است. چرا که با توجه به تعریف اشتراک مجموعه، هر عضوی که در اشتراک دو مجموعه وجود دارد، در هر یک از آنها نیز موجود است. بنابراین داریم:
A∩B⊆A و A∩B⊆B
نکته 3: خاصیت جابجایی مجموعه ها را که فراموش نکرده اید، این خاصیت در خصوص اشتراک دو مجموعه نیز صدق می کند.
A∩B = B∩A
مثال اشتراک دو مجموعه
1- اگر A={1,7,9} و B={2,7,19,9} باشد، A∩B را به دست آورده و نمودار وِن آن را رسم کنید.
حل: ابتدا اعضای مشترک هر دو مجموعه را مشخص می کنیم. دو عدد 3 و 8، هم در مجموعۀ A وجود دارند و هم در مجموعۀ B. بنابراین A∩B برابر است با:
A∩B={7,9}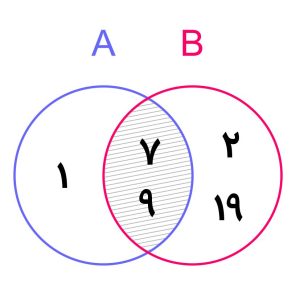
2- اگر مجموعۀ مضارب طبیعی عدد 4 را با M و مجموعۀ مضارب طبیعی عدد 3 را با N نمایش دهیم، M∩N را مشخص کنید.
حل: M∩N برابر است با مجموعۀ اعدادی که هم مضرب 4 هستند و هم مضرب 3. بنابراین M∩N برابر است با مجموعۀ مضارب طبیعی عدد 12. می‌توانیم M∩N را با استفاده از نماد‌های ریاضی به صورت زیر نمایش دهیم: M∩N={12k|k∈N}
حالت خاص اشتراک دو مجموعه
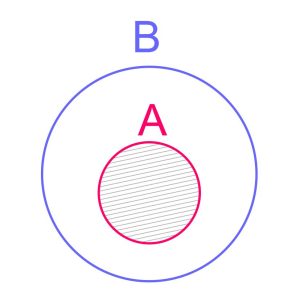
اگر برای دو مجموعۀ A و B داشته باشیم A⊆B، آنگاه اشتراک دو مجموعه چه خواهد شد؟
برای به دست آوردن اشتراک دو مجموعه به دنبال عضوهایی هستیم که در هر دو مجموعه تکرار شده اند، یعنی اعضایی که هم در A و هم در B وجود داشته باشند. با توجه به صورت مساله متوجه می شویم که تمام اعضای A، در مجموعه B نیز وجود دارند و عضو آن هستند. بنابراین داریم: A∩B=A
نمودار ون برای این حالت خاص از اشتراک مجموعه ها که یکی از مجموعه ها زیرمجموعه دیگری می باشد، به این شکل است:
تفاضل مجموعه ها ریاضی نهم
مجموعۀ A منهای B برابر است با کلیه اعضایی که عضو مجموعه A هستند ولی عضو مجموعه B نیستند. برای راحتی کار می توانید کلیه اعضای مشترک بین این دو مجموعه را از مجموعه A حذف کنید. مجموعه A−B را به زبان ریاضی به این صورت نمایش می دهند.
A−B={x|x∈A و x∉B}
نکته 4: خاصیت جابجایی در تفاضل مجموعه ها صدق نمی کند و A−B با B−A برابر نیستند.
مثال تفاضل دو مجموعه
1- اگر A={1,5,9} و B={12,5,10,9} باشد، A–B و B–A را به دست آورده و نمودار وِن آن را رسم کنید.
A−B برابر است با مجموعه {1}. چرا که 5 و 9 اعضای مشترک بین هر دو مجموعه هستند و اگر از مجموعه A حذف شوند فقط عدد 1 باقی می ماند.
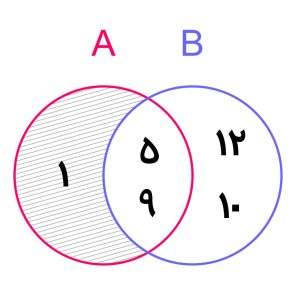
از طرفی اگر اعداد 5 و 5 را از مجموعۀ B حذف کنیم، مجموعۀ B−A به دست می‌آید. یعنی مجموعۀ B−A برابر است با {12,10}. نمودار ون مجموعۀ B−A نیز به شکل زیر است: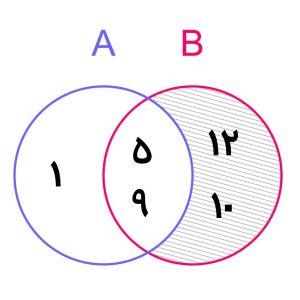
محصولات مرتبط
نظرات
1 دیدگاه برای اجتماع، اشتراک و تفاضل مجموعه ها
این سایت از اکیسمت برای کاهش هرزنامه استفاده می کند. بیاموزید که چگونه اطلاعات دیدگاه های شما پردازش می‌شوند.
یاسین –
سلام خانم معلم. مثالی که در مورد تفاضل مجموعه ها زدین و نمودار ون اون رو رسم کردین. کلا مشکل منو در درس اجتماع اشتراک ریاضی نهم حل کرد.😀😀😍
مهسا زنده دل –
سلام یاسین جان
هدف من هم همین هست که در درس اجتماع اشتراک و تفاضل مجموعه ها نهم هیچ اشکالی نداشته باشید و این درس رو خیلی خوب یاد بگیرید.