جواب تمرین صفحه 22 ، 27 و 31 ریاضی نهم
در ادامه ویدئوهای رایگان 20شو که قسمتی از پکیج آموزش ریاضی نهم به حل تمرین های صفحه 22،27 و 31 فصل دوم ریاضی نهم می رسیم. در کنار تماشای ویدئوی حل تشریحی تمرینات فصل دوم ریاضی نهم، می توانید برای یادگیری بیشتر و بهتر، از توضیحات ذیل کمک بگیرید.
جواب تمرین صفحه 22 ریاضی نهم ( درس اول فصل دوم )
تمرینات صفحه 22 ریاضی نهم مربوط به مبحث اعداد گویا از درس اول فصل دوم ریاضی نهم هست. البته برای یادگیری بیشتر و حل تمرینات متنوع تر می توانید از صفحه نمونه سوال فصل دوم ریاضی نهم کمک بگیرید.
1- حاصل عبارت های زیر را به دست آورید و تا حد امکان ساده کنید.
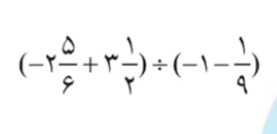
حل: برای ساده کردن این عبارت گویا، همیشه اولویت با عبارت داخل پرانتز هست. ابتدا اعداد مخلوط داخل پرانتز را به کسر تبدیل می کنیم. قبلاً یاد گرفته اید که برای تبدیل عدد مخلوط به کسر ابتدا باید عدد 2 را در مخرج یعنی 6 ضرب کنید و حاصل را با صورت کسر یعنی 5 جمع کنید و عدد به دست آمده را در صورت کسر بنویسید و مخرج را 6 قرار دهید. به این نکته هم دقت کنید که علامت منفی در پشت کسر قرار می گیرد و برای کل کسر است. مانند تصویر زیر.
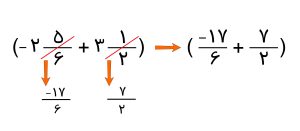
در این مرحله یک عبارت با دو عدد گویا داریم که می توانیم برای حل کردن آن از مخرج مشترک استفاده کنیم. که عبارت زیر به دست می آید.
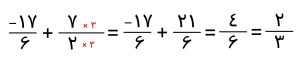
حالا به سراغ پرانتز دوم می رویم. برای اینکه بتوانید این عبارت را ساده کنید باید عدد 1- را به کسر تبدیل کنید. سپس دو عدد گویای به دست آمده را ساده کنید. مانند تصویر زیر:
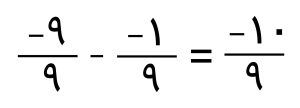
سپس دو پرانتز را که ساده کرده اید، دوباره بنویسید.
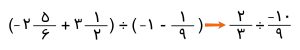
می دانید که برای تقسیم اعداد گویا و کسری، کسر اول نوشته می شود و تقسیم به ضرب تبدیل می شود،کسر دوم به صورت معکوس نوشته می شود.
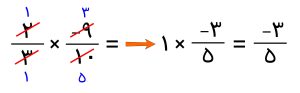
حال به سراغ ساده کردن عبارت ذیل می رویم.
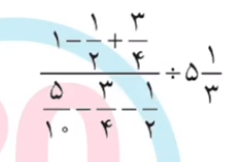 ترجیحاً ابتدا عبارت گویای صورت کسر اول را ساده می کنیم. برای این کار از مخرج مشترک استفاده می کنیم.
ترجیحاً ابتدا عبارت گویای صورت کسر اول را ساده می کنیم. برای این کار از مخرج مشترک استفاده می کنیم.
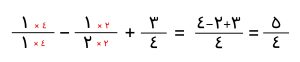
در مرحله بعد به سراغ ساده کردن اعداد گویای مخرج کسر می رویم. برای این کار بین کسرها باید مخرج مشترک بگیریم. می دانیم که ک م م مشترک بین این سه کسر برابر است با 20.
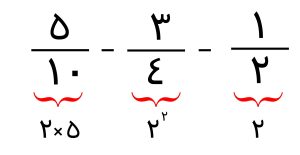
ک م م : پایه های مشترک با بیشترین توان ضرب در پایه های غیر مشترک
بعد از مخرج مشترک گیری عبارت را ساده می کنیم.
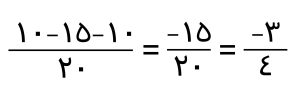
عدد مخلوط را هم به کسر تبدیل می کنیم و عبارت را یکبار دیگر بازنویسی کرده و مجدد ساده می کنیم.
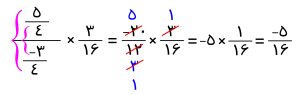
عبارت بعدی که در تمرین صفحه 22 ریاضی نهم آمده و باید ساده کنیم به این صورت است.
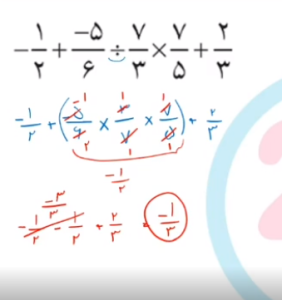
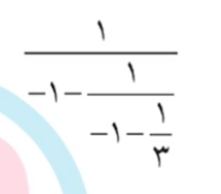
کسر بعدی یک کسر مرکب است. اگر در مورد کسرهای مرکب یا کسر مسلسل اطلاعاتی ندارید می توانید به ویدئوی آموزش کسر مرکب ریاضی هشتم رجوع کنید.
برای حل کسر مرکب باید از کوچکترین خط کسری شروع به حل کردن بکنید.
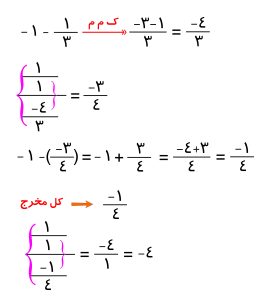
2- عبارت های زیر را از کوچک به بزرگ مرتب کنید.
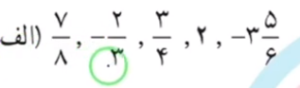
برای مرتب کردن این عبارت ها از کوچک به بزرگ اول به سراغ اعداد منفی می رویم. در بین اعداد منفی هر عددی که ظاهر بزرگتری داشته باشد در واقع کوچک تر است. در بین اعداد مثبت هم برای مشخص شدن اعداد کوچک تر، با استفاده از مخرج مشترک گیری، آنها را هم مخرج می کنیم و از این طریق به راحتی عبارت کوچک تر را تشخیص می دهیم. به همین راحتی می توانید از کوچک به بزرگ بنویسید.
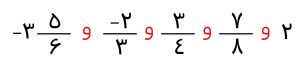
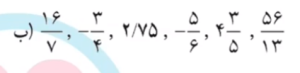
برای تشخیص کسرهای کوچکتر، توصیه می کنم به توضیحات گفته شده در ویدئوی آموزش جواب تمرین صفحه 22 ریاضی نهم که در ابتدای صفحه آمده است، به دقت نگاه کنید.
![]()
سوال 3 تمرین صفحه 22 ریاضی نهم فصل دوم
3- بین دو کسر، سه کسر بنویسید.
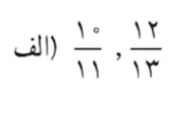
برای نوشتن کسر بین این دو کسر ابتدا بین دو کسر مخرج مشترک می گیریم.
![]()
در این مرحله یک کسر مابین دو کسر پیدا شد و آن را نوشتیم. برای نوشتن دو کسر دیگر، کسر اول و آخر را هم صورت و هم مخرح در 2 ضرب می کنیم و 2 کسر هم مابین این دو کسر پیدا می شود.
![]()
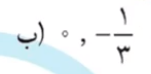
جواب:
![]()
جواب تمرین صفحه 27 ریاضی نهم ( تمرین درس دوم فصل دوم )
1- با توجه به مجموعه های داده شده، سایر سطرها را مانند سطر اول کامل کنید.
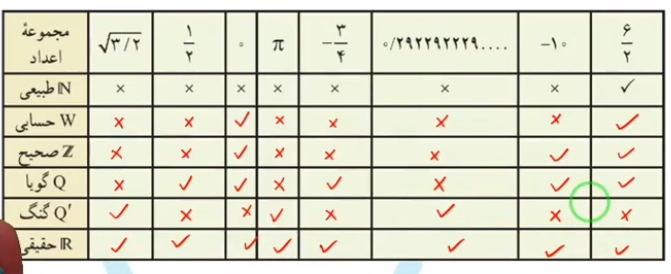
۲- در هر یک از حالت های الف و ب تفاوت دو مجموعه را با ذکر دلیل بنویسید.

مجموعه A، اعداد حقیقی بین 1.5 و 5 را نشان می دهد.
مجموعه B، اعداد گویا بین 1.5 و 5 را نشان می دهد.

مجموعه D، اعداد حقیقی بین 3 و 9 را نشان می دهد.
مجموعه C، اعداد طبیعی بین 3 و 9 را نشان می دهد.
3- طرف دوم تساوی های زیر را کامل کنید.
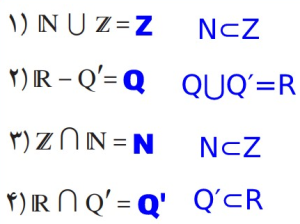
۴- عدد ۵√ + ۱ بین کدام دو عدد صحیح متوالی قرار دارد؟
عدد ۵√ بین دو عدد مربع کامل 4√ و 9√ قرار دارد. پس جواب به این صورت خواهد بود.

۵- بين هر دو عدد، چهار عدد گنگ بنويسيد.
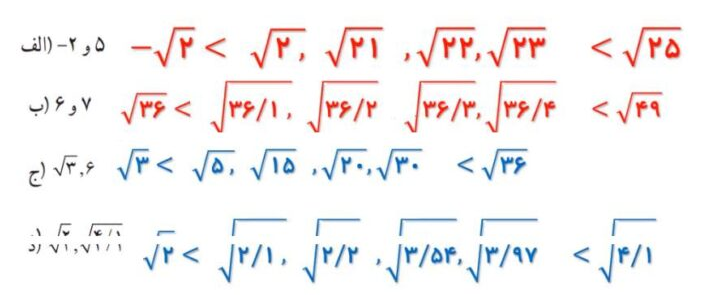
۶- عبارات درست را با ✔ و عبارات نادرست را با × مشخص کنید. برای عبارات درست مثال بزنید.

۷- در نمایش اعشاری عدد ۱۰√ و عدد ۳/۱۱ چه تفاوتی هست؟
√۱۰ = ۳/۱۶۲۲۷۷۶۶۰۱۶۸۳۷
۳/۱۱ = ۰/۲۷۲۷۲۷۲۷۲۷۲۷۲۷
در جواب رادیکال ده هیچ الگوی تکرار شونده ای نیست اما در جواب کسر سه یازدهم عدد ۲۷ بعد از ممیز تکرار می شود.
جواب تمرین صفحه 31 ریاضی نهم
1- اگر  و
و 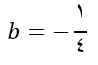 و
و 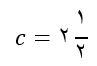 باشد، حاصل عبارت زیر را به دست آورید.
باشد، حاصل عبارت زیر را به دست آورید.
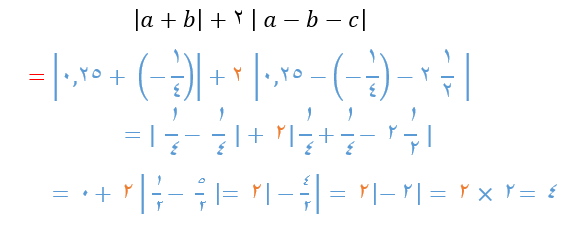

3- جای خالی را با عدد مناسب پر، و جواب هایتان را در کلاس با سایر دوستانتان مقایسه کنید:

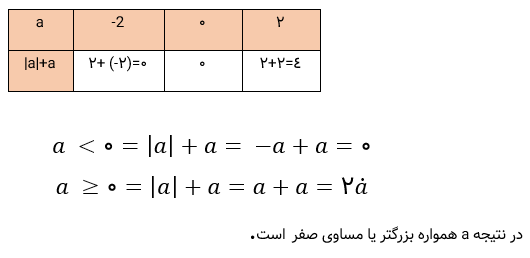
4- مقدار عددی عبارت a + [a] را به ازای a=−۲ و a=۰ و a=۲ به دست آورید. آیا می توانید عدد حقیقی به جای a قرار دهید که حاصل ![]() منفی باشد؟
منفی باشد؟
5- با ارائه یک مثال، نادرست بودن تساوی a2 = a√ را نشان دهید.
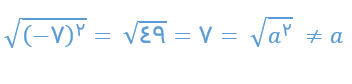
6- حاصل عبارات روبه رو را به دست آورید:











هنوز بررسیای ثبت نشده است.